1. Алгебра
  2. Вычислите производную функции

Вычислите производную функции y(x)=ctgx и найдите ее значение при x=п/6

Милошка28 Милошка28    1   02.06.2019 18:00    3

Ответы
MUSIC555 MUSIC555  03.07.2020 11:58

y'=({\rm ctg}\, x)'=-\dfrac{1}{\sin^2x}

Производная функции в точке x = п/6: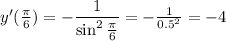 y'(\frac{\pi}{6})=-\dfrac{1}{\sin^2\frac{\pi}{6}}=-\frac{1}{0.5^2}=-4

ПОКАЗАТЬ ОТВЕТЫ
Gay1122 Gay1122  03.07.2020 11:58

Функция ctg x считается одной из элементарных, поэтому для нахождения ее производной можно воспользоваться таблицей производных:

f'(x) = (ctg x)' =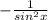 -\frac{1}{sin^{2}x }

Найдем значение производной в точке π/6:

y'(\pi/6)=-\frac{1}{sin^{2}\frac{\pi }{6} }=-\frac{1}{{(\frac{1}{2}) }^{2}}=-\frac{1}{\frac{1}{4} } =-4

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
tsisarmaria tsisarmaria  17.08.2021 19:33
Необходимо покрасить пол в комнате, длина которой 6 м, что на 200 см больше её ширины масляной краской два раза. В первый раз на каждый квадратный метр уходит 125 грамм...
Зайчонок512 Зайчонок512  17.08.2021 22:23
(3x-5y+2)^2 По какой формуле надо решать?...
veraeliseeva718 veraeliseeva718  17.08.2021 22:32
Точки О, К і М лежать на одній прямій. Знайдіть відстань між точками О і М, якщо ОК-8,2 см, КМ = 7,3 см. Скільки розв язків мае задача ​...
Motia2k17 Motia2k17  06.11.2020 11:28
Решите умоляю вас целую в лобик...
elyp28 elyp28  06.11.2020 11:28
Корень из 9 - 16 -7 корень из 0,36 + 5,4...
СветланаРассвет СветланаРассвет  08.12.2021 17:16
2. Розв яжи рівняння. а) y(у – 6) — (у – 11)? =y– 1; 6) 5x(x – 3) - 5(x - 2)2 = 15....
KatyaKerina KatyaKerina  08.12.2021 17:14
Sin 2x cos 5x - sin 3x cos 4x =0 Решите уравнение...
tan1978 tan1978  08.12.2021 17:13
Применяя формулу ньютона-лейбница вычислить данный определённый интеграл...
stacezoloto stacezoloto  01.04.2020 13:07
Найдите корень уравнения 2=2017х...
dobromirovamar dobromirovamar  01.04.2020 13:06
16k^2 − l^2 = если что, l = Л...

Популярные вопросы