1. Алгебра
  2. Вычислите площади плоских фигур,

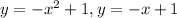
Вычислите площади плоских фигур, ограниченных линиямиy=-x^{2} +1,y=-x+1

MIO05 MIO05    1   09.11.2021 02:25    0

Ответы
Захар1191928 Захар1191928  09.11.2021 06:00

\frac{1}{6} кв.ед

Объяснение:

приравняем чтоб найти точки пересечения

-x^2+1=-x+1\\-x^2+x=0\\x(x-1)=0\\x_1=0\\x_2=1

построим график (фото)

1) y=-x^2+1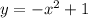 ветви вниз

парабола

Вершина параболы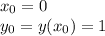 x_0=0\\y_0=y(x_0)=1

2) y=-x+1

прямая

по рисунку видно a=0, b=1

чтобы найти площадь того участка, мы большую площадь параболы, и отнимем меньшую площадь прямой в промежутке от 0 до 1, и ограниченной y=0

F(x)=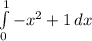\int\limits^1_0 {-x^2+1} \, dx

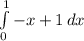
G(x)=\int\limits^1_0 {-x+1} \, dx

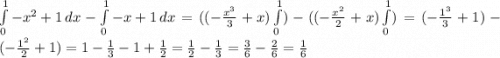S=F(x)-G(x)=\int\limits^1_0 {-x^2+1} \, dx -\int\limits^1_0 {-x+1} \, dx =((-\frac{x^3}{3}+x)\int\limits^1_0)-((-\frac{x^2}{2} +x)\int\limits^1_0)=(-\frac{1^3}{3}+1)-(-\frac{1^2}{2}+1)=1-\frac{1}{3}-1+\frac{1}{2}=\frac{1}{2} -\frac{1}{3}=\frac{3}{6}-\frac{2}{6}=\frac{1}{6} кв. ед.


Вычислите площади плоских фигур, ограниченных линиями
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
magauiyaa magauiyaa  30.05.2023 21:43
Завдання на фото терміново прлшу вас...
ОксанаБ80 ОксанаБ80  30.05.2023 21:42
Знайдіть кут між векторами АВ і CD, якщо А (1; 0; 2), В (1; 3; 3), С (-1; 0; 3), D (-1; -1; 3)....
Pump2000 Pump2000  30.05.2023 21:41
До іть бдлск Укажіть проміжок, який містить усі корені рівняння:...
sauleshka3 sauleshka3  22.09.2019 16:40
Найдите без построения точки пересечения с осями координат у=1,2х-24...
Farys Farys  22.09.2019 16:40
Решить уравнение только не нужно избавляться от 7x ,не превращайте в уравнение высших порядков...
misterion10 misterion10  22.09.2019 16:40
Найдите произведение первых пяти членов прогрессии учитывая что произведение её второго и четвёртого члена равно 144...
Холзи14 Холзи14  22.09.2019 16:50
Разложите на множители: 1) 4a(4c−13)+7(13−4c) 2) 2c(5c−8)−9(8−5c) 3) b(b+11)−3(−11−b)...
givka1 givka1  02.05.2020 16:02
Решите графическим а) 2х ²=3х+5 б) 1/Х=-Х+1...
Лиса0399 Лиса0399  02.05.2020 16:02
7. Установіть відповідність 1 .f(x) = 1,5х + 22. f(x) =x² +6х+93. f(x) =⅓x³- 3x²+8x-4 4. f(x) = -6х + 3,5х? - ⅔x³ a) (г( ; 1,5) 1 [2; 4)​...
LeНин LeНин  02.05.2020 16:02
Площа прямокутника дорівнює 675см2 . Знайди ширину прямокутника, якщо одна зі сторін на 12 см менша від іншої....

Популярные вопросы