Вычислите площадь фигуры,ограниченной линиями y = 3x2 , y = 0 , x = -3 , x = 2.
Ответы
Фигура ограничена: сверху кривой у = 3х², снизу прямой у = 0, слева прямой х = -3, справа прямой х = 2 (см. также рисунок). Поэтому находим определённый интеграл от -3 до +2.
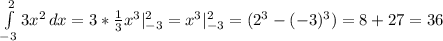
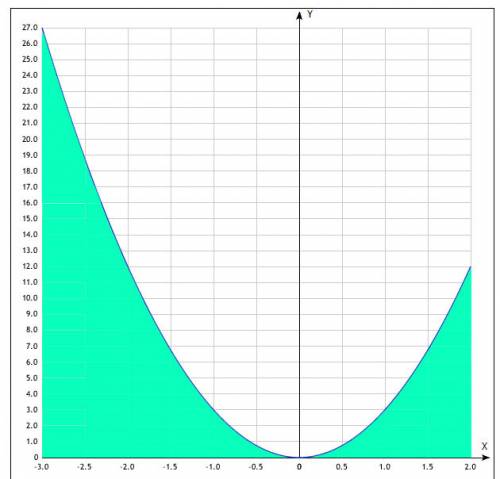
ПОКАЗАТЬ ОТВЕТЫ
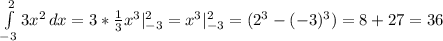

Другие вопросы по теме Алгебра
Популярные вопросы
- Четыре электронных слоя и один на электрон на внешнем слое имеет элемент :...
3 - Выполните превращения по схеме: zn → zns → h2s → so2 → so3...
1 - Площадь треугольника ace равна 90. на стороназ ac и ce треугольника взяли точки...
2 - Четыре бригады ремонтировали дорогу на четырех участкахнайди общую длину дороги...
2 - Заполните пропуски глаголом “tobe “ в нужной форме. 1. you speak english fluently....
1 - Твір-мініатюра на тему пісні мого краю...
3 - Против течения реки катер целую 49/50 за 1 целую 2/5 ч. а по течению 51 целую...
1 - Почему слово русалка пишем с маленькой...
3 - Із двох міст,відстань між якими 924км,виїхали назустріч один одному два автобуси.швидкість...
3 - Захоронение опасных веществ, возможные экологические риски...
2