1. Алгебра
  2. Вычислите площадь фигуры,

Вычислите площадь фигуры, ограниченной линиями f(x) = 2cosx, y=0, x=0, x= 3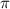\pi/2

mawa18 mawa18    2   15.01.2022 21:16    3

Ответы
бомба15682 бомба15682  15.01.2022 22:00

Площадь криволинейной трапеции вычисляется по формуле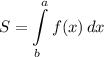   \displaystyle S=\int\limits^a_b {f(x)} \, dx

y=2cosx\ ,\ \ y=0\ ,\ x=0\ ,\ x=\dfrac{3\pi }{2}

По графику видно, что область от х=0 до х=3П/2 разбита на две области. Одна находится выше оси ОХ при изменении х от 0 до П/2 , а вторая находится ниже оси ОХ при х от П/2 до 3П/2 . Поэтому при вычислении определённого интеграла по второй области получим знак минус, а значит, чтобы площадь выражалась положительным числом, перед интегралом надо поставить знак минус .  

\displaystyle S_1=\int\limits_0^{\frac{\pi }{2}}\, 2\, cosx\, dx=2\cdot sinx\Big|_0^{\frac{\pi}{2}}=2\cdot (sin\dfrac{\pi}{2}-sin0)=2\cdot (1-0)=2S_2=-\int\limits_{\frac{\pi }{2}}^{\frac{3\pi }{2}}\, 2\, cosx\, dx=-2\cdot sinx\Big|_{\frac{\pi}{2}}^{\frac{3\pi}{2}}=-2\cdot (sin\dfrac{3\pi}{2}-sin\frac{\pi}{2})=-2\cdot (-1-1)=4S=S_1+S_2=2+4=6


Вычислите площадь фигуры, ограниченной линиями f(x) = 2cosx, y=0, x=0, x= 3/2
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Сахарокcom Сахарокcom  12.03.2021 17:30
33. Построить график функции и указать, внутри каких координат- ных углов расположен этот график:1) у=-1/3х3) y =4,5х;2) y =1/3х 4) у = -4,5х.34. Построить график функции:​...
malckowdanilр malckowdanilр  12.03.2021 17:29
Решите задачу с составление уровнения,разность двух чисел равна 34 а разность их квадратов - 408,найдите эти числа )...
солнышко279 солнышко279  12.03.2021 17:28
. Нужно найти наибольшее и наименьшее значение функций. 1. a) y=2x^3-3x^2 на промежутке (-1;3) b) y=5x^3-15x на промежутке (-2;2) 2. то же самое задание. a) y=x^3-3x^2 на промежутке...
Марина17681 Марина17681  12.03.2021 17:28
Найдите стороны и периметр прямоугольника, одна сторона которого меньше 3 см, а другая 180 см² Формула:у=а(х-m)²+a a≠0 ​...
kola56 kola56  12.03.2021 17:28
в кружок записались пятиклашки шестиклсшки семиклашки в отношении 1:2:5 всего в кружке 36 человек сколько,семиеласников в кружке...
yuliadruzhko yuliadruzhko  12.03.2021 17:26
Квадратне рівняння ах^2+bх+с=0 називають неповним, якщо… а) a = 0, b ≠ 0, c ≠ 0 б) a ≠ 0, b = 0, c ≠ 0 в) a ≠ 0, b ≠ 0, c = 0 г) a = 0, b ≠ 0, c = 0 д) a ≠ 0, b = 0, c = 0 Оберіть...
MaxineCaulfield2003 MaxineCaulfield2003  12.03.2021 17:25
2. Докажите, что значение выражения: 54³ – 24³ делится на 30​...
viparistocrate viparistocrate  05.10.2021 22:30
Виконайте дії a 3y-1 5-8y + y² y²b x²+3 3-x - x³ 3xв 2а+в - 4aв 20+вг. 3 3 2x + + х+3 x²-3x y-x²...
Tanya22rus Tanya22rus  05.10.2021 22:03
(a+b)×c при а=1, b=-3, c=2...
kisslenkayaozax1i kisslenkayaozax1i  05.10.2021 21:53
изобразите на координатной прямой промежуток -2 3 и запишите неравенство множеством решений которого он служит...

Популярные вопросы