Вычислите определенный интеграл:
a) 
b) во вложениях
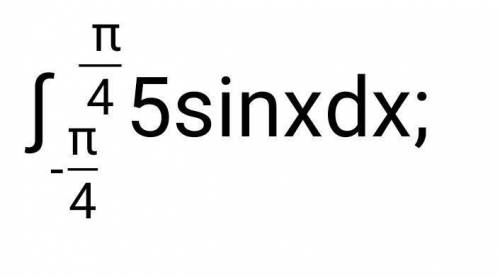
Другие вопросы по теме Алгебра
Популярные вопросы
- До іть будь ласочка, дуже сильно з геометрії (((...
2 - 2.обьём прямоугольного параллеледапипеда равен V см3 , одна сторона его основания...
2 - 5- 6. Астанада өткен «ЭКСПО-2017» көрмесі туралы ізденіп, кестені тол-гетырыңдар.НКөрмеде...
3 - Помгите сделать русский СОЧ Задание 1 1. Выпишите из текста 6-8 ключевых слов/словосочетаний....
3 - Task 4. Complete the text with was, were, wasn t or weren t. It was a terrible...
1 - Складіть харчовий ланцюг і визначте , скільки га вико-вівсяного поля потрібно...
1 - Біржасушалы организмдер түрлер саны...
1 - ДЕFP – прямоугольный, 2P = 90°. Сделай чертеж и заполните пропуски....
1 - Поясніть чому на екваторі і полюсі різна джі?...
2 - (cosx - cosy)² - (sinx - siny)²=-4sin x-y/2*cos(x+y)...
1
ответ: а) 10,5 ; b) 0
Решено от :