1. Алгебра
  2. Вычислите: lim(стремится к +беск)3n/n+2

Вычислите: lim(стремится к +беск)3n/n+2 lim(стремится к +беск)n^2\2n^2-1 lim(стремится к +беск)2n^2-1\n^2+5 lim(стремится к +беск)n^3+n\n^2-1 lim(стремится к +беск)2-n\3-n^2 lim(стремится к +беск)n^2-1\n^3+n

msvichinevskay msvichinevskay    3   17.06.2019 15:10    0

Ответы
dsg189g dsg189g  02.10.2020 03:47
Простые числа типа 1, 2, 3 можно убирать в пределах с бесконечностью(т.к. они очень маленькие по сравнению с бесконечностью и на ответ не влияют)

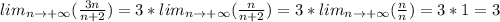
lim_{n\to+\infty}(\frac{3n}{n+2})=3*lim_{n\to+\infty}(\frac{n}{n+2})=3*lim_{n\to+\infty}(\frac{n}{n})=3*1=3

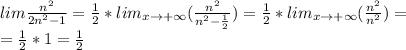
lim\frac{n^2}{2n^2-1}=\frac{1}{2}*lim_{x\to+\infty}(\frac{n^2}{n^2-\frac{1}{2}})=\frac{1}{2}*lim_{x\to+\infty}(\frac{n^2}{n^2}})=\\=\frac{1}{2}*1=\frac{1}{2}

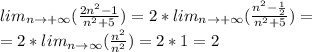
lim_{n\to+\infty}(\frac{2n^2-1}{n^2+5})=2*lim_{n\to+\infty}(\frac{n^2-\frac{1}{2}}{n^2+5})=\\=2*lim_{n\to\infty}(\frac{n^2}{n^2})=2*1=2

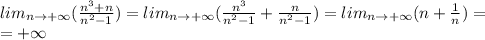
lim_{n\to+\infty}(\frac{n^3+n}{n^2-1})=lim_{n\to+\infty}(\frac{n^3}{n^2-1}+\frac{n}{n^2-1})=lim_{n\to+\infty}(n+\frac{1}{n})=\\=+\infty

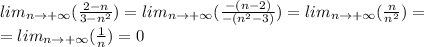
lim_{n\to+\infty}(\frac{2-n}{3-n^2})=lim_{n\to+\infty}(\frac{-(n-2)}{-(n^2-3)})=lim_{n\to+\infty}(\frac{n}{n^2})=\\=lim_{n\to+\infty}(\frac{1}{n})=0

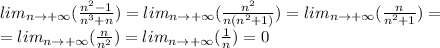
lim_{n\to+\infty}(\frac{n^2-1}{n^3+n})=lim_{n\to+\infty}(\frac{n^2}{n(n^2+1)})=lim_{n\to+\infty}(\frac{n}{n^2+1})=\\=lim_{n\to+\infty}(\frac{n}{n^2})=lim_{n\to+\infty}(\frac{1}{n})=0
ПОКАЗАТЬ ОТВЕТЫ
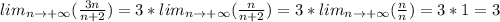
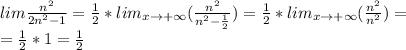
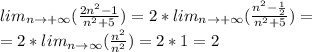
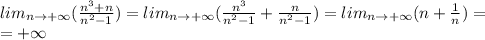
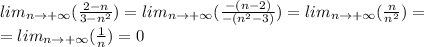
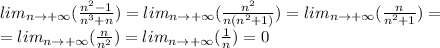
Другие вопросы по теме Алгебра
proulechka proulechka  11.08.2019 17:10
Укажите значение р, при которых равно нулю значение дроби р²-3р-10 деленое на р-3р²...
irynafurmanets irynafurmanets  11.08.2019 17:10
Прямая задана уравнением 6х-у=-3 укажите значения коэфициентов к и м при которых данная прямая и прямая заданная уравнением у=кх+м...
Нвб Нвб  11.08.2019 17:10
Выяснить является ли функция четной или нечетной : у=|х|-соsx...
minikolp12344 minikolp12344  11.08.2019 17:10
Докажите, что середины сторон равнобедренного треугольника являются также вершинами равнобедренного треугольника. , нужно обязательно с табличкой: дано: решение: найти:...
braununs braununs  11.08.2019 17:10
Постройте график функции заданой формулой: а)y=-2x+1 б)y=0,2x+5 в)y=-x+4,5 г)y=x+1,5...
aidaadilbekova aidaadilbekova  11.08.2019 17:10
Решите уравнение: 2 cos (п/4 - x/2) = 1...
vanyad09 vanyad09  11.08.2019 17:10
Преобразуйте уравниние 2х-у-3=0 к виду линейной функции у=кх+м. чему равны к и м...
Gok3004 Gok3004  11.08.2019 15:03
Решите и опишите уравнение подробно 3х2-х-4=0 ....
Legendary13 Legendary13  11.08.2019 15:23
Нужно! решите неравенство : 5^(х+2/х)-1/2*10^(х+1/х)+2^(1/х)-5^(1/х) 0...
yfcnz1215 yfcnz1215  11.08.2019 15:27
Определить по рисунку наименьшую по абсолютной величине градусную меру углов aob, aoc, aod, aoe.(тригинометрия)...

Популярные вопросы