Вычислите, буду благодарен
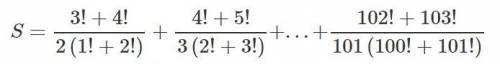
Другие вопросы по теме Алгебра
Популярные вопросы
- Аможет выполнить б за 10 часов, а б может выполнить а за 20 часов. при совместной...
1 - Найти песню, знаю только слова, нужно ,,простите но я выбрал её ,я её выбирал...
2 - Напишите ответ. вверху написано . заранее ....
3 - 1.наибольшее давление в сосуде бывает при его расширении или сужении? 2.постоянный...
1 - Камень, массой 1кг, без начальной скорости падает с высоты 10м. кинетическая...
2 - Відрізок вм медіана трикутника авс. на продовженні відрізка мв за точку в позначили...
3 - Надеюсь найдутся знатоки: ) им отдельный респект и огромное...
3 - Ididn t do it yesterday. i it yet. we bought the tickets on monday. we already...
3 - Какие документы надо для поезда? что-то по типу паспорта или сведительства о...
2 - Скакой силой, направленной вдоль ледяной горы, надо тянуть тело массой 100 кг...
2
Ряд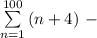 арифметическая прогрессия, у которой
арифметическая прогрессия, у которой
Вторая строчка в числителе первое слагаемое (n+2)!