Вычислите 15tg(arccos 3/√34).
Другие вопросы по теме Алгебра
Популярные вопросы
- Адмірал Бенбоу» – це.Острів Скарбів 6 клас...
1 - Забейте, лучше заберите :D...
3 - W - -бұл суреттерден не көріп отырсыңдар?-нелер бейнеленген ?-қандай...
3 - одна сторона параллелограмма в 5 раз больше другой а его периметр...
1 - КОНТРОЛЬНАЯ 2.Tick () the sentences which contain the correct form...
3 - 1.Кто из будущих декабристов принимал участие в разработке «Устава...
1 - найдите СИНОНИМЫ и антонимы...
2 - Выпишите в два столбика слова: 1 — чередование звуков происходит...
1 - Решите контрольную по английскому, негде ответов нет, как можно...
2 - Определите части стебля: 1: (ответ) 2: (ответ) 3: (ответ) 4: (ответ)...
3
(см. объяснение)
Объяснение:
Найдем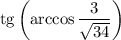 :
:
Найдем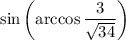 :
:
Тогда:
Итого:
Задание выполнено!