Алгебра: Вычислите: 1) arccos(sin()) 2) arctg(ctg())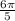

Вычислите: 1) arccos(sin( $\frac{8\pi }{7\\}$ ))
2) arctg(ctg( $\frac{6\pi }{5}$ ))

Ответы

AndreevaAS2 14.04.2021 03:34

$1) \ arccos\left(sin\frac{8\pi}{7} \right)=\frac{9\pi}{14} \\ \\ 2) \ arctg\left(ctg\frac{6\pi}{5} \right)=\frac{3\pi}{10}$

Объяснение:

по формулам приведения:

$sinx=cos\left(\frac{\pi}{2}-x \right) \\ \\ ctgx=tg\left(\frac{\pi}{2}-x \right)$

Также необходимо знать, что

$arccos(cosx)=x, \ 0\leq x\leq \pi \\ \\ arctg(tgx)=x, \ -\frac{\pi }{2} < x< \frac{\pi }{2}$

$1) \ arccos\left(sin\frac{8\pi}{7} \right) =arccos\left(cos \left(\frac{\pi}{2}- \frac{8\pi}{7} \right)\right) =arccos\left(cos \left(- \frac{9\pi}{14} \right)\right)=(*)$

Но -9π/14 не находится на отрезке от 0 до π. A 9π/14 как раз принадлежит этому отрезку. Значит воспользуемся свойством четности косинуса:

cos(-x)=cosx

Тогда продолжая цепочку, получаем:

$(*)=arccos\left(cos\frac{9\pi}{14}\right)=\frac{9\pi}{14} \\ \\ 2) \ arctg\left(ctg\frac{6\pi}{5}\right)=arctg\left(tg\left(\frac{\pi}{2}-\frac{6\pi}{5}\right)\right)=arctg\left(tg\left(-\frac{7\pi}{10}\right)\right)=(*)$