вычислить сумму членов ряда.
Другие вопросы по теме Алгебра
Популярные вопросы
- Решить: молекулярное, полное и краткое ионное уравнение nicl2+naoh...
1 - 3класс что такое преобразование фигур...
2 - Производственная программа на год - 35000 деталей. норма расхода материала...
3 - Підмет виділенно у реченні а ) я стежу за хмарами . ловлю їх світлий...
3 - Тело нагрели на 20 градусов. это изменение температуры в градусах к...
1 - Велосепедист увеличил скорость на 10 % и стал ехать на 1,5 км в час...
2 - Буква ю обозначает два звука в слове...
3 - План развития отношения татьяны и онегина? надо,а.с пушкин...
3 - На конференции присутствовало 288 учёных, из которых 5/8 - , а остальные...
3 - Сочинение на тему: почему люди пишут стихи?...
2
Здесь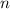 -й член ряда
-й член ряда 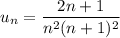 является правильной рациональной дробью относительно
является правильной рациональной дробью относительно 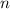 . Разложим
. Разложим 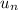 на сумму простейших дробей:
на сумму простейших дробей:
Если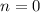 , то
, то 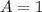
Если , то
, то 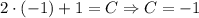
Коэффициенты около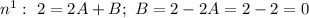
Коэффициенты около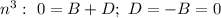
Итог: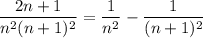
Поэтому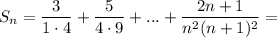
Следовательно,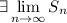 , ряд сходится, а сумма ряда
, ряд сходится, а сумма ряда 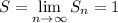
ответ: 1.