Вычислить пределы функции.
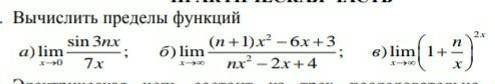
Другие вопросы по теме Алгебра
Популярные вопросы
- очень , I wish I so scared, but I do! Jake s mum wishes he so much money on clothes...
2 - Составить 5 предложений на there is l/are и there was/aere...
2 - Үзіндідегі құбылтудың түрін ажыратып, талдаңыз: Салқын шымда тұрып бабы келіскен...
2 - Подписать 2 любых острова, 2 полуострова, 2 архипилаги. Контурная карта по географии...
1 - B. Шустрые частицы(любой язык программирования) Ограничение времени 1 секундаОграничение...
1 - Выскажите предложение о том Почему военные преступления рассматривать не только...
3 - Що означає запис: 4H,7CO2,K2O,CI,6Cu,6Cl2,SiO2,2H2...
2 - Дан равнобедренный треугольник LMN с основанием MN точка P выбрана на стороне...
1 - Хозяин дачного участка строит баню с парным отделением. Парное отделение имеет...
2 - Скажите ответ нужен дайте больше нету...
2
Объяснение:
Неопределённость 0/0.
Возьмём производную одновременно от числителю и знаменателя:
Неопределённость ∞/∞.
Разделим одновременно числитель и знаменатель на х²: