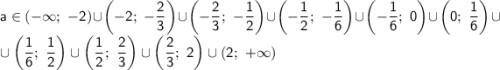Вычислить по каких действительных значениях а уравнение имеет 4 корня
Другие вопросы по теме Алгебра
Популярные вопросы
- Начерти прямоугольник длина которого 8 см а ширина на 2 см короче вычисли...
1 - Почему стеклянная колба с ртутью имеет тонкие стенки?...
1 - Прочитай и перескажи текст. найди предложение, выражающее главную мысль текст....
2 - Составить диалог в фотостудии на украинском языке...
1 - :tиісті жалғауларды қойып, көшіріп жазыңдар. 1.біздің қазақстан республикасы....
1 - 4x-2y=3 13x+6y=-1 решите систему уравнений...
2 - 33 ! ! я вас ! классифицировать знаки препинания(выделительные, разделительные,...
2 - Какую роль как наука, играет в развитии общества?...
3 - Снапишите информацию, о которой тебя просят. 1. write 5 subjects you have...
2 - Рассказ о разнообразии мира природы по картине дерево жизни...
3
Раскладываем числитель и знаменатель на множители
В итоге исходное уравнение запишется как
В числителе имеем 4 корня, но в связи с ограничениями по ОДЗ (x≠-1/2; x≠2), требуется исключить следующие случаи
А еще исключим возможность повторения корней
ответ: