Вычислить по формулам Муавра
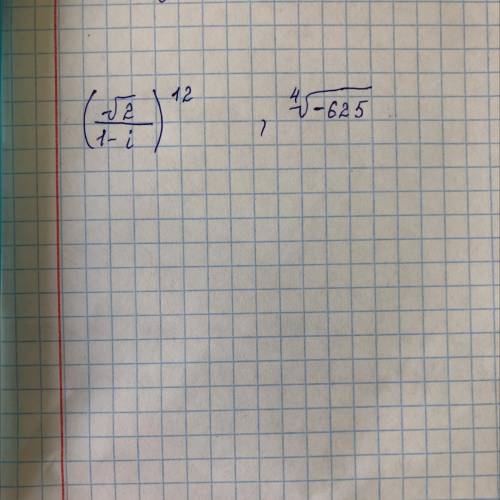
Другие вопросы по теме Алгебра
Популярные вопросы
- 1. Увлечение (мото) (вело) спортом, получить (радио) грамму, заниматься...
1 - Виды физической культуры? Выберите один ответ: a. Базовая (образовательная),...
2 - Напишите цепочку ядерных превращений аргона: β, β, β, α, α, β, α,...
3 - Какие ассоциации возникают? Что может связывать эти иллюстрации?...
2 - Өсімдіктердің тыныс алу процесі Мен Фотосинтез процесін салыстырыңыз...
1 - Помагите Броун қозғалысы». Оқушылардан электронды кітапханадан нешекітап...
1 - 3 класс русский язык страница 8 упражнения 1 Я рисую...
2 - Расстояние между двумя городами–w км из них одновременно навстречу...
3 - ВАС РЕШИТЕЕЕ,УМОЛЯЯЮЮЮЮ ВСЕБАЛЛЫ ДАЮ ВАММ РЕШИТЕЕЕ ОЧЕГЬ ВАЖНОООООУМОЛЯЯЮЮЮЮ...
1 - Твір роздум в художньом чтилі...
1
Объяснение:
Пусть
Формула Муавра имеет вид: