Вычислить неопределенный интеграл x cos 2x dx
Другие вопросы по теме Алгебра
Популярные вопросы
- . Турция и Иран в начале 20 века. Нужно кратко написать про каждую страну....
2 - Задание 1 Choose the correct spelling: 1. attitude atitude attitud 2. see...
2 - a) Was kann man alles in den Sommerferien machen! Schreibe deine 10 Tipps...
3 - Какие правила должен соблюдать каждый ученик при входе в компьютерный класс?...
1 - На рисунке 299 изображена траектория движения шарика, переместившегося из...
1 - Там будет лишь омытый дождём мокрый луг под огромным небом, да несколько деревьев...
3 - Мотоцикл и автобус начинают движение с точки с координатой 10, мотоцикл движется...
1 - Анапируем сравниватаРассмотрите и сравните две разные ситуации посадкиза компьютером....
3 - Успіху якого моря розташоване місто Венеція, де жив Марко поло...
3 - Сколько раз повтвряется число 8 в одназначных и двухзначных числах...
3
Объяснение:
Воспользуемся методом интегрирования по частям: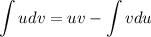
Пусть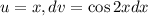 . Тогда
. Тогда 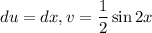 . Получаем:
. Получаем: