Вычислить наиболее рациональным значение выражения.
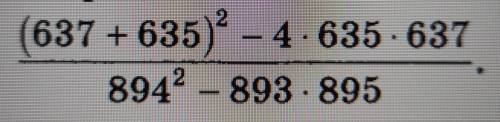
Другие вопросы по теме Алгебра
Популярные вопросы
- Постоянные признаки и непостоянные признаки слова ,,глубокой...
1 - Условия потенциальную опасность возникновения чс...
1 - Які закони механіки належать до загальних законів природи...
2 - Кто или что такое парламент? только ответ для 3 класса...
3 - Поясните поговорку все дороги ведут в рим...
3 - Почему римские власти враждебно относились к христианам...
2 - Найдите значение параметра p при которых уравнение x2 + 10x - 5p=0 имеет единственный...
3 - Что является главной художника при создании портрета?...
3 - Выберите словосочетания в неопределенной форме 1 ) работает добросовестно.2)приятно...
3 - Решите : одна двенадцатая + одна третья × (0,84: 0,8-1,8)...
3
(см. объяснение)
Объяснение:
Рассмотрим числитель дроби:
Рассмотрим знаменатель дроби:
Тогда ответом будет число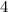 .
.
Задание выполнено!
Комментарий:
На самом деле задача примитивна и, судя по виду, придумана для учеников 7-ых классов. Действительно, здесь мы видим две простейшие формулы сокращенного умножения.
В числителе - это:
А в знаменателе наблюдается: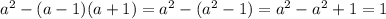
Данные формулу очень удобны, что демонстрирует данный пример. Однако важно заметить их неединственность. Необходимо изучить все, чтобы быть готовым к любы аналогичным заданиям.
4.
Объяснение:
((637+635)² - 4•637•635)/(894² - 893•895) = 4.
1. Упростим числитель:
((637+635)² - 4•637•635) =
= 637² + 635² + 2•637•635 - 4•637•635 =
= 637² + 635² - 2•637•635 = (637 - 635)² =
= 2² = 4.
2. Упростим знаменатель:
894² - 893•895 = 894² - (894-1)(894+1) =
= 894² - (894²-1²) = 894² - 894² + 1² = 1.
3. Найдём значение дроби:
4/1 = 4 : 1 = 4.
В процесса решения использованы формулы:
(a±b)² = a² ± 2ab + b² и
а² - b² = (a-b)(a+b).