Вычислить, используя формулу муавра
Другие вопросы по теме Алгебра
Популярные вопросы
- Фермер наметил собрать с поля 12т овощей , а собрал 7/6 этого количесва...
3 - Сколько людей проживало в середине 16 века в великом новгороде?...
2 - Вкакой части материка течет река оранжевая...
1 - Вбукете 4 розовых цветка и3 белых какую часть всех цветков составляет...
2 - Какие вопросы можно задать ветерану вов...
2 - Скажите какие растения красной книги на чёрных страницах...
2 - Глубины мах. и мин. азовского моря (вывод глубокое или мелкое) то...
1 - Скорость ракеты 8 км/с. за сколько минут она пролетит 960 км...
1 - Дополнить предложение однородными членами: все взволнованно говорили...
1 - Найдите в каждой строчке лишнее слово и объясните почему оно тёмный,...
3
Положим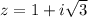 . Модуль комплексного числа:
. Модуль комплексного числа: 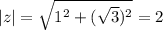 ,тогда
,тогда 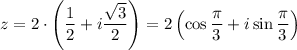
По формуле Муавра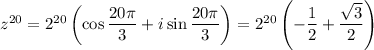
Аналогично, положим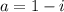 , тогда
, тогда 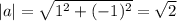 , тогда
, тогда 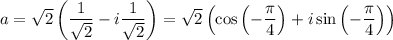
Тогда по формуле Муавра
Окончательно получаем