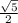Вычислить ctgα, если sin〖α= 2/3〗; π/2<α< π
Другие вопросы по теме Алгебра
Популярные вопросы
- Чему равно ускорение свободного падения на Марсе? Масса Марса 6,4·֗1020кг, радиус...
3 - На рисунке 18 указаны в некоторой системе отсчёта направления скорости и ускорения...
2 - Нарисуйте автомобиль, стоящий на середине выпуклого моста. Изобразите силы действия...
2 - Вспомните закон всемирного тяготения и запишите его формулу...
1 - На каком расстоянии от Земли сила притяжения тела к Земле равна силе его притяжения...
2 - Чему равна первая космическая скорость у поверхности Луны, если радиус Луны 1,7·֗103км,...
3 - Заполните таблицу, записав в неё выражение для веса тела и рассмотрев различные...
1 - Какую перегрузку испытывает космонавт массой 70 кг при старте космического корабля,...
1 - С какой силой давит автомобиль массой 1 т на середину выпуклого моста, имеющего...
3 - Заполните таблицу, сравнив силу тяжести, действующую на тело, и его вес....
1
Объяснение:
sin α = 2/3.
π/2<α< π - , угол α расположен во второй четверти. . Значит, его косинус отрицателен.
Из основного тригонометрического тождества sin²a+cos²a=1 следует, что:
cos α = −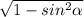 = -
= - 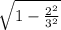 = -
= - 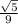
Значения ctga находим через sina и cosa по формуле:
ctgα = = -
= -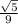 :
:  = -
= -