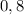Вычислить cos x, если sin x = 0.6 когда 0<х<пи/2 Возможные ответы
0.6, - 0.6 0.8 и - 0.8
Другие вопросы по теме Алгебра
Популярные вопросы
- Нужно умоляю выполните . выберите верные суждения. отметьте их в таблице...
2 - Придумайте проблемную ситуацию к творческому проекту умный дом...
2 - Почему говорят, что облачный покров - это одеяло земли?...
1 - Назвать героические и эпические оперы композиторов....
2 - Просклоняй и меня существительные. выдали окончания. р.п. стол сосна д.п....
2 - Определите тип реакций, расставте коэфиценты в схемах h2+ n2 - nh3 h2o -...
1 - Примеры воздействия музыки на человека...
1 - Напишите два объявления о приёме в танцевальную студию: одно- строгое,в...
3 - Подскажите сказку про имя существительное. надо...
1 - Вванне 200л воды. сколько раз в ванну поместится кубик со строной 1м?...
1
Используем основное тригонометрическое тождество: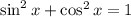
Откуда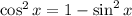
Значение находится в пределах от
находится в пределах от 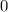 до
до 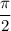 , что соответствует его расположению в первой координатной четверти, а функция косинус в первой координатной четверти положительна, поэтому:
, что соответствует его расположению в первой координатной четверти, а функция косинус в первой координатной четверти положительна, поэтому:
ответ: