1. Алгебра
  2. Вычислить arcsin(sin 141pi/16)

Вычислить arcsin(sin 141pi/16)

Олeксандра Олeксандра    1   14.07.2020 00:18    1

Ответы
илья1864 илья1864  30.08.2020 13:22

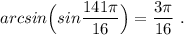
ответ:   arcsin \Big(sin \dfrac{141\pi }{16}\Big)=\dfrac{3\pi }{16}\ .

Решение.

\boxed {\ arcsin(sinx)=x\ , \ esli\ \ -\dfrac{\pi}{2}\leq x\leq \dfrac{\pi}{2}\ \ ili\ \ -90^\circ \leq x\leq 90^\circ \ }\\\\\\\arcsin\Big(sin\dfrac{141\pi}{16}\Big)=arcsin \Big(sin\Big(8\pi+\dfrac{13\pi }{16}\Big)\Big)=arcsin\Big(sin\dfrac{13\pi}{16}\Big)=

=\Big[\ \dfrac{13\pi }{16}=146,25^\circ\in (90^\circ ;180^\circ )\notin (-\90^\circ ;90^\circ )\Big]=\\\\=arcsin\Big(sin\Big(\pi -\dfrac{3\pi }{16}\Big)\Big)=arcsin\Big(sin\dfrac{3\pi }{16}\Big)=\Big[\ \dfrac{3\pi }{16}=33,75^\circ \in (-90^\circ ;90^\circ )\ \Big]=\\\\=\dfrac{3\pi }{16}

ПОКАЗАТЬ ОТВЕТЫ
лоллрр лоллрр  30.08.2020 13:22

Вычислить arcsin(sin(141π/16)

ответ:   3π/16 .

Объяснение:  - π/2 ≤ arcsin(a) ≤  π/2

sin141π/16 =sin(9π- 3π/16 )= sin(3π/16) .

* * * 3π/16=(π/2)*(3/8)  < π/2 * * *

arcsin(sin(141π/16) =arcsin(sin(3 π/16)  =3π/16.

sin(141π/16) =sin(8π+ 13π/16)= sin(13π/16)= sin(π -3π/16) =sin(3π/16) .

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
GoodSmileEweryDay GoodSmileEweryDay  22.07.2019 02:30
Умнику нужно было сложить с некоторым числом 26. вместо этого он вычел из этого числа 26 и в результате получил число 14. какое число он должен был получить...
никокотрик никокотрик  22.07.2019 02:30
Медведь поручил волку сосчитать количество зверей в лесу: медведей ,волков ,зайцев и выяснить кого из больше и на сколько.после подсчета волк доложил: 1.всего зверей 100. 2.волков...
жмлпр жмлпр  22.07.2019 02:30
Числа x,y и z таковы ,что x2yz3=711 и xy2=7 чему равно xyz...
blinovaa blinovaa  22.07.2019 02:30
Первая труба пропускает на 4 литра воды в минуту меньше, чем вторая. сколько литров воды в минуту пропускает первая труба, если резервуар объемом 396 литров она заполняет на...
Dendizevs Dendizevs  22.07.2019 02:30
Заготовили 32,5т овса. сначала израсходовали 0,4 этого запаса ,а потом две третьи остатка. сколько тонн овса осталось после этого ? объясните как решать ,...
никита3427 никита3427  19.09.2019 13:10
Преобразуйте в многочлен стандартного вида: а) (a+1)^3= б) (4-b)^3=...
akur12 akur12  19.09.2019 13:10
Здраствуйте нужна 1. решить уравнение : (х+6)² - (х-5) (х+5) = 79; 2. подайте в виде произведения выражение: (4b-9)² - (3b+8)². 3. выражение (3-b) (3+b) (9+b²) + (4+b²)² и найдите...
Бос2017 Бос2017  19.09.2019 13:10
Sin(α-2π)*cos (3/2π-α)+tg(π-α)*tg(3/2π+α)+cos^2(π\2-α) выражение...
daryaromanovsk daryaromanovsk  19.09.2019 13:10
Надо разложить на умножители : 1) 14-14m(в квадрате) 2)3а-3а(в кубе) 3) 7х(в пятом степени)-7ху(в квадрате)...
FarHowl FarHowl  19.09.2019 13:10
Решите уравнение с объяснением: (5x+2)^2-(3x+5)^2=0...

Популярные вопросы