Выберите три правильные утверждения.
1 областью значений функции у = 7ˣ + 2 является промежуток [2, + ∞).
2 областью определения функции у = log₂ (х² + 1) является множество действительных чисел.
3 уравнение (√3) = 1 не имеет корней.
= 1 не имеет корней.
4 если основание и пидлогарифмичний выражение поменять местами, то значение логарифма log₂ 8 уменьшится втрое.
5 число -2 в виде логарифма по основанию 5 - это log₅ 0,04.
6 если f( х) = log ₀,₅ ₓ х, то f( π) > f( 3).
7 число 81 является решением неравенства log₂ log₃√ₓ ≥ 1
(виберіть три правильні твердження.
1 областю значень функції у = 7ˣ + 2 є проміжок [ 2; + ∞).
2 областю визначення функції у = log₂( х²+ 1) є множина дійсних чисел.
3 рівняння (√3) = 1 не має коренів.
= 1 не має коренів.
4 якщо основу і підлогарифмічний вираз поміняти місцями, то значення логарифма log₂ 8 зменшиться втричі.
5 число –2 у вигляді логарифма за основою 5 – це log₅ 0,04.
6 якщо f( х) = log ₀,₅ ₓ х, то f( π) > f( 3).
7 число 81 є розв’язком нерівності log₂ log₃√ₓ ≥ 1)
Другие вопросы по теме Алгебра
Популярные вопросы
- Решите турист 2 1/7ч шел пешком и 3 3/5ч ехал на велосипеде. расстояние,которое...
3 - Қатысу- етістікті тауып морфология талдау...
2 - Решить: )(тригонометрия) надо 1) 2)...
2 - Снада 1) укажите два пследовательных целых числа, между которыми заключено число...
3 - Сколько книг написала дарья донцова...
1 - Найти число: 13\15 которого равны 195 решение:...
3 - Провести полное исследование функции y=(9+6x-3x^2)/(x^2-2x+13)...
3 - Составь изапиши предложения с этими словами.укажи части речи,и их грамматическое...
2 - Найдите высоту ромба,периметр которого равен 124 см, а площадь 155 кв. см...
3 - I( chatter to feed the animals. i learned to ride ahorse. when it ( sunny, i...
1
Область значений функции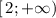 - неверное утверждение.
- неверное утверждение.
ООФ - множ. действ. чисел - верное утверждение.
Уравнение не имеет корней - неверное утверждение, уравнение как раз имеет два корня.
Значение выражения уменьшится втрое - неверное утверждение, оно уменьшится в 3:(1/3)=9 раз.
верное утверждение
х=81 входит в область решений неравенства , значит утверждение верно