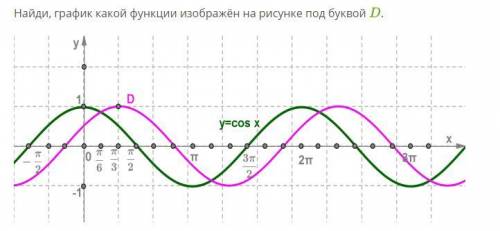
Выбери правильный ответ:
y=2cosx
y=cosx−3
y=cos(x−π4)
y=cos(x+π3)
y=cos(x+π4)
y=cosx+2
y=−cosx+3
y=cos(x−π3)
y=cosx−2

Для решения данного вопроса нужно сравнить график функции y=cos(x) с графиками остальных вариантов ответа.

График функции y=cos(x) является графиком косинусной функции и имеет форму периодической кривой, осциллирующей между значениями -1 и 1. График периодичен с периодом 2π и имеет точку минимума при x=0 и точку максимума при x=π.

Рассмотрим каждый вариант ответа по очереди:

1) y=2cosx: данная функция лишь умножает график y=cos(x) на 2, что приводит к растяжению функции вверх и вниз вдвое. График по-прежнему осциллирует между -2 и 2. Таким образом, это неверный ответ.

2) y=cosx−3: данная функция вычитает из графика y=cos(x) константу 3, что приводит к смещению графика вниз на 3 единицы. График по-прежнему осциллирует между -4 и -2. Таким образом, это неверный ответ.

3) y=cos(x−π/4): данная функция осуществляет горизонтальное смещение графика y=cos(x) на π/4 вправо. Это означает, что точка минимума теперь будет при x=π/4, а точка максимума - при x=5π/4. График по-прежнему осциллирует между значениями -1 и 1. Таким образом, это верный ответ.

4) y=cos(x+π/3): данная функция осуществляет горизонтальное смещение графика y=cos(x) на π/3 влево. Это означает, что точка минимума теперь будет при x=-π/3, а точка максимума - при x=4π/3. График по-прежнему осциллирует между значениями -1 и 1. Таким образом, это неверный ответ.

5) y=cos(x+π/4): данная функция осуществляет горизонтальное смещение графика y=cos(x) на π/4 влево. Это означает, что точка минимума теперь будет при x=-π/4, а точка максимума - при x=7π/4. График по-прежнему осциллирует между значениями -1 и 1. Таким образом, это неверный ответ.

6) y=cosx+2: данная функция добавляет к графику y=cos(x) константу 2, что приводит к вертикальному смещению графика вверх на 2 единицы. График по-прежнему осциллирует между 1 и 3. Таким образом, это неверный ответ.

7) y=−cosx+3: данная функция умножает график y=cos(x) на -1 и затем добавляет константу 3, что приводит к вертикальному смещению графика вверх на 3 единицы и отражает его относительно оси x. График по-прежнему осциллирует между 2 и 4. Таким образом, это неверный ответ.

8) y=cos(x−π/3): данная функция осуществляет горизонтальное смещение графика y=cos(x) на π/3 вправо. Это означает, что точка минимума теперь будет при x=π/3, а точка максимума - при x=4π/3. График по-прежнему осциллирует между значениями -1 и 1. Таким образом, это неверный ответ.

9) y=cosx−2: данная функция вычитает из графика y=cos(x) константу 2, что приводит к смещению графика вниз на 2 единицы. График по-прежнему осциллирует между -3 и -1. Таким образом, это неверный ответ.

Итак, правильный ответ на данный вопрос - y=cos(x-π/4).