Вурне 10 белых и 10 черных шаров. все шары из урны извлекаются парами, причем
вынутые шары обратно не возвращают. какова вероятность того, что все пары будут
состоять из разноцветных шаров.
Другие вопросы по теме Алгебра
Популярные вопросы
- Непомню квк делать пунктационый разбор !...
2 - Дифракционная решетка находится на расстоянии l = 0,12 м от экрана. при освещении...
3 - Обьясните где и как образуется первичная мача...
1 - Найдите значение производной функции: f(x)= 1+4x/1+2x, при х=1...
2 - Уподаних нижче нормативно-правових актах розставте порядковим номером послідовності...
3 - Найдите промежутки возрастания и убывания функции: x=1/2x + x/2. заранее ! )...
2 - Какое количество теплоты выделится в сопротивлением 200 ом, включенном в сеть...
3 - Хорды ab и cd пересекаются в точке p. найдите длину хорды cd если известно что...
1 - 1) xимия огэ 22, даны вещества : медь, соляная кислота, растворы : сульфат мели...
3 - Решение с остатком 37: 7 44: 7 65: 7 83: 7 220: 7...
3
Пусть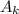 (k = 1,2,...,n) - k-ая пара состоит из разноцветных шаров.
(k = 1,2,...,n) - k-ая пара состоит из разноцветных шаров.
Вероятность выбрать первую пару из разноцветных шаров равна
В урне остается 9 белых и 9 черных шаров. Вероятность выбрать вторую пару из разноцветных шаров равна
Вероятность выбрать третью пару из разноцветных шаров равна
...
...
...
Вероятность выбрать девятую пару из разноцветных шаров, равна
Вероятность выбрать десятую пару из разноцветных шаров, равна
Искомая вероятность по теореме умножения
ответ: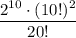 .
.