1. Алгебра
  2. Второй член прогрессии

Второй член прогрессии равен 4, а отношение суммы квадратов ее членов к сумме ее членов 16/3. найти сумму первых 3 членов прогрессии.

mamutova0303 mamutova0303    2   27.09.2019 02:01    1

Ответы
MariaVay000 MariaVay000  08.10.2020 21:38

b_{2} =b_{1}q=4

\frac{{b_{1}^{2}+b_{2}^{2}+...b_{n}^{2}}}{b_{1}+b_{2}+...b_{n}}=\frac{16}{3}

Если нужно найти сумму первых 3 членов, то ограничимся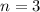 n=3

n=3; b_{1}, b_{2}=b_{1}q, b_{3}=b_{1}q^{2}

b_{1}+b_{2}+b_{3}=b_{1}(1+q+q^{2})=b_{1}(q^{2}+q+1)

b_{1}^{2}, b_{2}^{2}=b_{1}^{2}q^{2}, b_{3}^{2}=b_{1}^{2}q^{4}

b_{1}^{2}+b_{2}^{2}+b_{3}^{2}=b_{1}^{2}+b_{1}^{2}q^{2}+b_{1}^{2}q^{4}=b_{1}^{2}(1+q^{2}+q^{4})

Представим уравнение 4 степени по-другому, выделив полный квадрат:

q^{4}+2q^{2}+1-q^{2}=(q^{2}+1)^{2}-q^{2}=(q^{2}+q+1)(q^{2}-q+1)

Из уравнения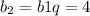 b_{2}=b{1}q=4 выразим b_{1}:

b_{1}=\frac{4}{q}

Получилось уравнение:

\frac{{b_{1}^{2}(q^{2}+q+1)(q^{2}-q+1)}}{b_{1}(q^{2}+q+1)}=\frac{16}{3}

b_{1}\frac{{(q^{2}+q+1)(q^{2}-q+1)}}{(q^{2}+q+1)}=\frac{16}{3}

Подставим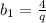 b_{1}=\frac{4}{q}:

\frac{{4(q^{2}+q+1)(q^{2}-q+1)}}{q(q^{2}+q+1)}=\frac{16}{3}

Откуда, сократив на 4 и на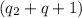 (q_{2}+q+1) получаем:

\frac{q^{2}-q+1}{q}=\frac{4}{3}

Домножим обе части на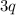 3q:

3(q^{2}-q+1)=4q

Раскрываем скобки:

3q^{2}-3q+3-4q=0

3q^{2}-7q+3=0

D=b^{2}-4ac=(-7)^{2}-4*3*3=49-36=13

q_{1}=\frac{7+\sqrt{13}}{6}

q_{2}=\frac{7-\sqrt{13}}{6}

далее найдёте сами сумму трёх первых членов

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
KATE4213 KATE4213  31.03.2019 22:22
7класс. . выражение затем найдите его числовое значение: ​...
Meowmeowmeow151 Meowmeowmeow151  31.03.2019 23:50
Выражение a( b+c-bc)-b(c+a-ac)+c(b-a)...
MaxHelpMelol MaxHelpMelol  31.03.2019 23:50
Какое из неравенств является неверным, если известно,что а b a) a+14 b+13 б) a-5 b-6 в) 8a 6b г) -4a -4b...
илья1899 илья1899  31.03.2019 22:26
Корень sinxcosx(1/tg2x+1)=0 решить уравнение с окружностями...
dshvedova06 dshvedova06  31.03.2019 22:29
1. 4,09⋅105 л = ⋅10 м3; 2. 54⋅102 км/ч = ⋅10 м/с; 3. 2,9⋅106м2 = ⋅10 га....
Портнягин Портнягин  31.03.2019 23:50
1.найти общий вид первообразной: а) f(x)=x^4-sin3x+5x б) f(x)=(3x+2)^3-4/x^6 2. высота цилиндра = 8дм., радиус основания = 5 дм. этот цилиндр пересечён плоскостью, параллельной...
entogenes entogenes  04.03.2021 22:37
Скільки існує три цифровых чисел, усі цифри яких парні​...
саня45рг саня45рг  04.03.2021 22:39
Решите неравенство2x - 1 9​...
Ромчик15 Ромчик15  04.03.2021 22:39
решить тригонометрическое уравнение...
досметова досметова  04.03.2021 22:42
Решите неравенство 7x - 12 ≤ 8x + 7​...

Популярные вопросы