Всем привет составить уравнение к задаче. Пытался со своим вариантом, но он не подходит:
Текст задачи:
В сосуд с чистой водой налили 6 литров 64%-ного (по объему) раствора спирта, а затем после полного перемешивания вылили равное количество (т.е. 6 литров) получившегося раствора. Сколько воды было первоначально в сосуде, если после троекратного повторения этой операции в сосуде получился 37%-ный раствор спирта?
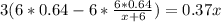
Другие вопросы по теме Алгебра
Популярные вопросы
- Напишите не большое про любого животного в мастацком -описании...
1 - Коля,дима и саша собрали вместе30грибов.дима нашел в два раза...
2 - Составить схему к 3-мя предложениям: 1.поклонились царевич и...
3 - Написать текст про папу и перевести на...
2 - Снеподвижной лодки прыгает человек массой 80 кг с горизонтальной...
3 - Сочинение на тему свободное время-прекрасное время на 1-2 листа...
2 - Одна сторона прямоугольника на 2см больше другой. найдите площадь...
2 - Вцилиндрический сосуд налили 3000см в кубе воды. уровеньводы...
2 - Що визначає характер і долю людини за романом айвенго...
3 - 2*(28/7)/6+39+(6*3)*(27/9)-14*3 реши пример...
2
Пусть х литров воды было в сосуде, добавили 6 литров спирта, значит в сосуде ( x+6) литров раствора, в котором 0,64·6=3,84 л чистого спирта.
Процентное содержание спирта:
(х+6) л составляет 100%
3,84 л составляют p%
Выливаем 6 литров, т. е в сосуде остается
х л % раствора
% раствора
Значит,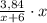 л чистого спирта
л чистого спирта
Повторяем процедуру три раза
1)
Доливаем первый 6 литров 64% спирта.
Получаем:
(х+6) л раствора, в котором
Выливаем 6 литров, т. е в сосуде остается
х л раствора, в котором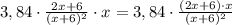 л чистого спирта.
л чистого спирта.
2)
Доливаем второй раз 6 литров 64% спирта.
Получаем:
(x+6) л раствора, в котором
л чистого спирта.
...
18 литров.
Объяснение:
Смотри решение на фото