ВОЗРАСТАЮЩАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ НАТУРАЛЬНЫХ ЧИСЕЛ Пусть a1, a2, ...,a11 - возрастающая последовательность натуральных чисел. Известно, что ai + aj +ak > as + at ,при i ≠ j ≠ k , s ≠ t
Каково наименьшее возможное значение суммы a1 + a2, ...+ a11 ?

242

Объяснение:

Наименьшее возможное значение суммы трёх неравных членов равно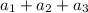 , наибольшее значение суммы двух членов равно 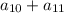. Значит, если для этих членов неравенство выполняется, то и для любых других гарантированно выполняется.

Два соседних числа отличаются как минимум на 1, значит,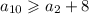 и .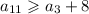

Наименьшее значение первого члена 17, тогда следующий член не меньше 18, третий - не меньше 19 и т.д.

Наименьшая сумма отсюда равна

если, конечно, последовательность 17, 18, ..., 27 удовлетворяет условию

Легко проверить, что эта последовательность подходит: действительно, 17 + 18 + 19 = 54 > 53 = 26 + 27