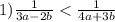Вноги кланяюсь решите ,не понимаю даже как начинать делатьзарание ☺☺☺☺
Другие вопросы по теме Алгебра
Популярные вопросы
- 1. воздушный шарик надули и отпустили. изменится ли объем шарика,...
2 - Составить текст с глаголами во 2 лице...
2 - том и сойра 5 глава краткое содержание...
1 - Сочинение как герда кая кратко...
2 - Запиши 5 сумм с одинаковыми первыми слагаемыми.найди их значения....
2 - Верёвку разрезали на 9 частей,не складывая её,сколько разрезов...
3 - Какие проверочные слова у запах сорняк охранять садовый...
1 - Разберите слова по составу рассмешил ,подоались,переливается,обошлось,перепрыгнуть,подсунуть,вынуть,взять,обуть,отойти...
3 - Запасы продуктов хватит 20 туристом на 4 дня на сколько хватит...
3 - Составить уравнения реакции, с которой можно осуществить следующие...
2
Известно, что 3a-2b и 4a+3b - положительные числа, причем
3a-2b > 4a+3b.
1) Если 3a-2b и 4a+3b - положительные числа, значит, их произведение (3a-2b)·(4a+3b) - положительное число.
2) По условию 3a-2b > 4a+3b - верное неравенство.
Разделим обе части этого неравенства на (3a-2b)·(4a+3b), при этом знак неравенства сохраняется, т.к. делим на положительное число.
Сократив, получим:
или
ответ под первым номером: