Виріште, будь-ласка, рівняння по логарифмам 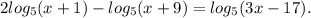
Другие вопросы по теме Алгебра
Популярные вопросы
- Яку невiстку хотiв мати герасим калитка з трагiкомедiï 100 тисяч ? , будь-ласка...
1 - Проверьте, правильно ли расставлены коэффициенты в уравнениях. по необходимости...
2 - Объяснить запятые 1)зима в феврале становится по-настоящему сердитой, ветер...
1 - Напишите уравнения реакций с которых можно осуществить следующие превращения:...
2 - 10 1) в основании прямой призмы находится равнобедренная трапеция, у которой...
2 - Решите ! 50 ! найдите значение выражения, если x+5y=4x+5y=4: ( 0,4x−2y ) : (...
1 - Краткая характеристика в сказке снежная королева (о чем идёт речь? )...
1 - Найдите диаметр круга,если площадь равна 14п кв.см...
3 - Местоимение как часть речи.дать определение. примеры. ....
2 - Переведите число 110100100 из двочной в десятичную систему счислений. с решением...
3
x=36
1) log5 x = 2log5 3 + 4 log25 2;
log5 x = log5 3² + 2log5² 2²; log5 x = log5 9 + log5 4;
log5 x = log5 (9.4); log5 x = log5 36;
Oтвет: x 36.
ОДЗ:
{х+1>0.
{х+9>0.
{3х-17>0.
х ∈ (17/3; +∞).
- - - - - - - - - - - - - - - - - - - - - - - - - - -
По т. Виета:
Откуда, х=-11 и х=7. Но корень х=-11 не подходит по ОДЗ.
ответ: х=7.