Вфигуру ограниченной пораболой у=8+2х-х2 и осью абсцисс вписан прямоугольник наибольшей площади две вершины которого расположены на параболе а другие две на оси абсцисс найдитеплощадь прямоугольника безумно буду

Абсцисса вершины параболы:

Xm = -b/(2a) = 1

Парабола симметрична относительно своей центральной оси, проходящей через указанную точку х = 1.

Выбираем произвольную точку х справа от х=1. Пусть это правая нижняя вершина искомого прямоугольника. Ее значение ограничено большим корнем уравнения:

8+2х-x²=0

Корни:  -2  и 4

Итак выбранная нами координата х принадлежит интервалу (1; 4)

Тогда длина прямоугольника из соображений симметрии относительно оси х = 1:

а = 2(х-1)

Высота прямоугольника равна ординате соответствующей точки параболы:

b = 8+2x-x²

Тогда площадь, как ф-ия от х:

S(x) = ab = 2(x-1)(8+2x-x²)

Находим производную и исследуем на монотонность и экстремумы:

S'(x) = 2[(8+2x-x²) + (x-1)(2-2x)] = 2[8+2x-x²+2x-2-2x²+2x]=2(-3x²+6x+6)=0

Критические точки: (1-√3)  и (1+√3)

Вторая точка как раз принадлежит интервалу (1; 4) и является точкой максимума.

Найдем площадь, подставив х = 1+√3  в ф-ию S(x):

Smax = 2*√3(8+2+2√3-1-2√3-3) = 12√3

ответ: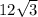 .