1. Алгебра
  2. Вероятность того, в квартиру

Вероятность того, в квартиру придет по заявлению комиссия из ЖЭКа, равна 0,3. Было подано 525 заявлений. Найти вероятность того, что количество обследованных квартир: а) равен 160 б) лежит в пределах от 150 до 155; в) меньше, чем 162.

1slishkomtupaya 1slishkomtupaya    3   12.06.2021 18:56    1

Ответы
пандочка94 пандочка94  12.07.2021 19:42

а)

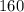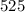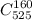Выбрать 160 квартир из 525 можно \displaystyle C^{160}_{525} . Вероятность, что именно эти 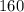160 квартир будут обследованы, составляет 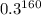0.3^{160}. Вероятность того, что все остальные квартиры не будут обследованы, 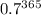0.7^{365}. Итого:

                                  C^{160}_{525} \cdot 0.3^{160} \cdot 0.7^{365} \approx 0.03675

б)

Понятно, что искомая вероятность - это сумма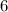 6 таких выражений, как в пункте а), только где 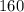160 заменено на 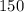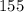150, ..., 155. То есть:

       C^{150}_{525} \cdot 0.3^{150} \cdot 0.7^{375} + C^{151}_{525} \cdot 0.3^{151} \cdot 0.7^{374} + C^{152}_{525} \cdot 0.3^{152} \cdot 0.7^{373} + \\\\+ C^{153}_{525} \cdot 0.3^{153} \cdot 0.7^{372} + C^{154}_{525} \cdot 0.3^{153} \cdot 0.7^{371} + C^{155}_{525} \cdot 0.3^{155} \cdot 0.7^{370}

Это примерно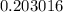 0.203016.

в)

Аналогично здесь получится:

        C^{0}_{525} \cdot 0.3^{0} \cdot 0.7^{525} + C^{1}_{525} \cdot 0.3^{1} \cdot 0.7^{524} + ... + C^{161}_{525} \cdot 0.3^{161} \cdot 0.7^{364}

Или:

                                      \displaystyle \sum\limits_{i=0}^{161} \,\,\, C_{525}^i \cdot 0.3^i \cdot 0.7^{525-i} \approx 0.65037

Задача решена!

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
nastylamyr2999 nastylamyr2999  25.11.2020 11:19
Выполнить задание: 1.Дана функция y = 2x – 3. Вычислите значения функции при x = -3 и x = 1. 2.Для функции y = -1,5x – 5. Найдите значение x, при котором y = 1. 3.Назовите...
Moldir94 Moldir94  25.11.2020 11:19
Задание 1.Прочитайте и озаглавьте текст. 3 б.Сформулируйте вопросы, которые передают отношение к ситуации, описанной в рассказе. 4 б.2.Письменно передайте основное...
Кейл Кейл  25.11.2020 11:19
Розкласти на множники МНОГОЧленкх-ук-уа+ха​...
fhuffggergryth5h6 fhuffggergryth5h6  25.11.2020 11:19
5. Представьте в виде трехчлена выражение -5(x-3)(х + 2). : 2 6. Упростите выражение (7n-1)(n+3) - 7n(n+4) и найдите его зна-3чение при п =8. Выполните деление: (18a*b...
lolipop891 lolipop891  25.11.2020 11:19
Определи (не выполняя построения) взаимное расположение графиков линейных функций у=8x+2 и нужно (можно полным ответом...
eleniuuum eleniuuum  25.11.2020 11:19
В амфитеатре 13 рядов. В первом ряду 17 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре...
marinovamari1 marinovamari1  17.12.2019 19:33
(x-8)(x+5) (x+6)^2 выполните действия и распишите чтобы я поняла❤...
nagimako nagimako  17.12.2019 19:31
График какой функции изображён на рисунке? gr4.png варианты ответов: y=1,5x−2 y=−23x−2 y=−3x−2 y=−2x−3...
AvroraMessi AvroraMessi  17.12.2019 19:31
Сколько целых решений имеет неравенство : |x-2| 5? ​...
228alex777 228alex777  17.12.2019 19:31
найдите вершину параболы и определите промежуток на котором функция убывает: y=x^2-8x...

Популярные вопросы