Важно сделайте ! докажите, что при всех значения переменной значение выражения положительно.
Ответы
С телефона не смогу но смысл в том, чтобы разложить знаменатель первой дроби по формуле разницы квадратов Получится 5^2-(б^2)^2=(5-б^2)(5+б^2) - это будет общий знаменатель этих 3 дробей И тогда привести к общему знаменателю все 3 дроби. Попробуй так.
ПОКАЗАТЬ ОТВЕТЫ
Если положительное это додатне тогда сейчас.
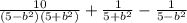 Первый дробь оставляем без изменений(ты это не пиши просто не могу написать формулами) второй домножаем на 5-
Первый дробь оставляем без изменений(ты это не пиши просто не могу написать формулами) второй домножаем на 5-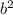 , третий домножаем на 5+
, третий домножаем на 5+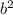 . Получиться:
. Получиться:
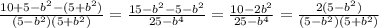 . 5-
. 5-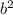 скорачиваем(убираем) то-есть выходит:
скорачиваем(убираем) то-есть выходит:
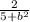 . Из этого выплывает, что все дилительные положительные числа, по-этому ответ тоже будет положительным. Так как
. Из этого выплывает, что все дилительные положительные числа, по-этому ответ тоже будет положительным. Так как 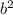 переменная, и находится в квадрате, означает, что при любом числе будет получаться положительное...
переменная, и находится в квадрате, означает, что при любом числе будет получаться положительное...
ПОКАЗАТЬ ОТВЕТЫ
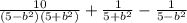 Первый дробь оставляем без изменений(ты это не пиши просто не могу написать формулами) второй домножаем на 5-
Первый дробь оставляем без изменений(ты это не пиши просто не могу написать формулами) второй домножаем на 5-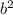 , третий домножаем на 5+
, третий домножаем на 5+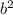 . Получиться:
. Получиться: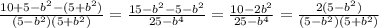 . 5-
. 5-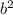 скорачиваем(убираем) то-есть выходит:
скорачиваем(убираем) то-есть выходит: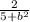 . Из этого выплывает, что все дилительные положительные числа, по-этому ответ тоже будет положительным. Так как
. Из этого выплывает, что все дилительные положительные числа, по-этому ответ тоже будет положительным. Так как 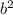 переменная, и находится в квадрате, означает, что при любом числе будет получаться положительное...
переменная, и находится в квадрате, означает, что при любом числе будет получаться положительное...
Другие вопросы по теме Алгебра
Популярные вопросы
- Оценка основных климатических показателей одного из регионов страны. дайте характеристику...
3 - Пионеры получили собрать 25 кг лекарственных трав‚ а собрали в 4 раза больше....
2 - Вчем заключались важнейшие перемены, произошедшие в период правления ивана грозного...
1 - Характеристика т. пейнакем был т. пейн что открыл, что сделал, как прославился,...
3 - Ввашем регионе найден новый источник сульфатной гидрокарбонатно-натриевой минеральной...
1 - Ac = 16x = ? 17 adcb. триогольник. что бы было данно и решение. 8 класс ...
3 - Перевести текст. глагол to be в трех формах (утверждение, вопрос, отрицание)...
1 - Используя интернет-ресурсы, найди музыку других композиторов на сюжет пиковая...
1 - Найти массовою долю практического выхода железа который образуется из-за оксида...
3 - написать письмо. недавно вы приняли участие в организации культурного мероприятия...
1