В урне содержится К шаров, среди которых могут быть черные и белые, к ним добавляют L белых шаров. После этого из урны случайным образом
вынимают М шаров. Найти вероятность того, что все вынутые шары белые,
предполагая, что все возможные предположения о первоначальном содержании урны
равновозможны.
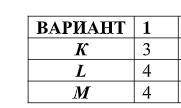
Значения параметров K, L и М по вариантам приведены в ТАБЛИЦА
Другие вопросы по теме Алгебра
Популярные вопросы
- паж (´ε` )♡ / ̄ ̄ \< ´・ \ | 3 ) \ < 、・ \ \__/∪ _∪ ) ...
3 - Напишите выражение для нахождения площади поверхности куба, используя...
3 - В пробирку наберите немного раствора азотной кислоты и, погрузив...
3 - Үш ңұсқаның ішінен қажетті сөзді таңдап номер 8...
2 - (2b^3-c^2)^2+(2b^3+c^2)(2b^3-c^2)...
1 - ПОМГИТЕ СОР ПО ГЕОГРАФИИ2 задание задачу 1-ую можно не не делать...
3 - Моё отношение к Игнатьичу(можете по своему)...
2 - из перечисленных выберете три реки которые относятся к бассейну Атлантического...
3 - Task 2. Write the missing words. Напиши пропущенные вопросительные...
2 - Синоним к словуудовлетворенность...
3
Для начала, давайте определим вероятность того, что первый шар будет белым. Так как в урне содержится K шаров, среди которых могут быть черные и белые, а к ним добавили L белых шаров, общее количество шаров стало равно K + L. Таким образом, вероятность того, что первый шар будет белым, равна L / (K + L).
Если первый шар оказывается белым, то в урне остается K черных и L - 1 белых шаров. Так как мы уже взяли один белый шар, количество белых шаров станет L - 1. Таким образом, вероятность того, что второй шар также будет белым, равна (L - 1) / (K + L - 1).
По аналогии, если первые M - 1 шаров были белыми, в урне остается K черных и L - (M - 1) белых шаров. Таким образом, вероятность того, что M-ый шар будет белым, равна (L - (M - 1)) / (K + L - (M - 1)).
Теперь мы можем записать вероятность того, что все вынутые шары будут белыми, используя формулу условной вероятности:
P(все шары белые) = P(первый шар белый) * P(второй шар белый | первый шар белый) * ... * P(M-ый шар белый | первые M - 1 шаров белые)
То есть,
P(все шары белые) = (L / (K + L)) * ((L - 1) / (K + L - 1)) * ... * ((L - (M - 1)) / (K + L - (M - 1)))
Теперь давайте применим эту формулу к каждому варианту из таблицы.
1) При K = 3, L = 6, M = 2:
P(все шары белые) = (6 / (3 + 6)) * ((6 - 1) / (3 + 6 - 1)) = 6/9 * 5/8 = 5/12
2) При K = 5, L = 4, M = 3:
P(все шары белые) = (4 / (5 + 4)) * ((4 - 1) / (5 + 4 - 1)) * ((4 - (3 - 1)) / (5 + 4 - (3 - 1))) = 4/9 * 3/8 * 3/7 = 9/56
3) При K = 4, L = 5, M = 4:
P(все шары белые) = (5 / (4 + 5)) * ((5 - 1) / (4 + 5 - 1)) * ((5 - (4 - 1)) / (4 + 5 - (4 - 1))) * ((5 - (4 - 1)) / (4 + 5 - (3 - 1))) = 5/9 * 4/8 * 3/7 * 3/6 = 5/84
4) При K = 2, L = 3, M = 2:
P(все шары белые) = (3 / (2 + 3)) * ((3 - 1) / (2 + 3 - 1)) = 3/5 * 2/4 = 3/10
5) При K = 4, L = 1, M = 3:
P(все шары белые) = (1 / (4 + 1)) * ((1 - 1) / (4 + 1 - 1)) * ((1 - (3 - 1)) / (4 + 1 - (3 - 1))) = 1/5 * 0/3 * 0/2 = 0
Таким образом, вероятность того, что все вынутые шары белые, в каждом из вариантов равна:
1) 5/12
2) 9/56
3) 5/84
4) 3/10
5) 0