В урне 3 белых, 2 красных, 1 черный шар, вынимают 2 шара. Найти вероятности: А – шары одного цвета; В – есть
ровно один черный шар.

Question

Алгебра: В урне 3 белых, 2 красных, 1 черный шар, вынимают 2 шара. Найти вероятности: А – шары одного цвета; В – есть ровно один черный шар.

nastyakarina112 · Answer

Общее количество вариантов выбрать 2 шара из 6 имеющихся равно числу сочетаний из 6 по 2:

$C_6^2=\dfrac{6!}{2!\cdot(6-2)!} =\dfrac{6\cdot5}{1\cdot2} =15$

Определим сколькими можно выбрать два шара одного цвета. Так как черный шар всего один, то это могут быть либо белые шары, либо красные. Выбрать 2 белых шара можно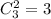 C_3^2=3 , а 2 красных шара - C_2^2=1 .

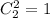Вероятность определим как отношение благоприятных вариантов к общему числу вариантов:

$P(A)=\dfrac{C_3^2+C_2^2}{C_6^2} =\dfrac{3+1}{15} =\boxed{\dfrac{4}{15}}$

Определим сколькими можно выбрать два шара так, чтобы один из них был черным. Если один шар черный, то другой можем выбрать из пяти оставшихся шаров, то есть всего существует 5 благоприятных вариантов.

Определяем вероятность:

$P(B)=\dfrac{5}{C_6^2} =\dfrac{5}{15} =\boxed{\dfrac{1}{3}}$