, В уравнении х2 -13х + q =0 один из корней равен 3. Найдите второй корень и коэффициент q

Ответы

raistarasenko 12.02.2022 11:50

ответ.

$x^2-13x+q=0\ \ ,\ \ x_1=3$

По теореме Виета, если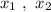 $x_1\ ,\ x_2$ - корни заданного квадр. уравнения,

то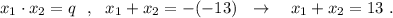 $x_1\cdot x_2=q\ \ ,\ \ x_1+x_2=-(-13)\ \ \to \ \ \ x_1+x_2=13\ .$

Заменим первый корень на 3 , получим $\left\{\begin{array}{l}3+x_2=13\\3x_2=q\end{array}\right$

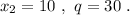
$\left\{\begin{array}{l}x_2=10\\3\cdot 10=q\end{array}\right\ \ \left\{\begin{array}{l}x_2=10\\q=30\end{array}\right$

ответ: $x_2=10\ ,\ q=30\ .$

ПОКАЗАТЬ ОТВЕТЫ

anfisakadnikova 12.02.2022 11:50

Теорема Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение - свободному члену с тем же знаком. и Обратная теорема Виета если угадаем числа, такие, что их сумма опять же для приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение - свободному члену с тем же знаком то эти числа - корни уравнения, при условии, что дискриминант неотрицателен.

По Виету сумма корней 13, один корень есть, тогда второй корень

13-3=10

и по тому же Виету произведение корней равно свободному члену q=3*10=30

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра