1. Алгебра
  2. В треугольнике с вершинами O(0,0,0),

В треугольнике с вершинами O(0,0,0), A(7,3,–5), B(–5,7,3) проведена биссектриса AОB. Написать ее каноническое уравнение с решением. Нужно подробное описание решения.


В треугольнике с вершинами O(0,0,0), A(7,3,–5), B(–5,7,3) проведена биссектриса AОB. Написать ее кан

michytka2305200 michytka2305200    1   09.01.2022 15:29    0

Ответы
burvan1987 burvan1987  16.02.2022 10:38

A(7;3;-5)\ ,\ B(-5;7;3)\ ,\ O(0;0;0)

Найдём направляющие векторы для ОА и ОВ .

\overline{OA}=(7;3;-5)\ \ ,\ \ |\overline{OA}|=\sqrt{49+9+25}=\sqrt{83}\\\\\overline{OB}=(-5;7;3)\ \ ,\ \ |\overline{OB}|=\sqrt{25+49+9}=\sqrt{83}

Эти векторы имеют одинаковые длины. Если на них построить ромб, то биссектрисы углов этого ромба будут лежать на его диагоналях (по свойствам ромба) . А диагонали ромба - это векторы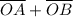  \overline{OA}+\overline{OB}  и  

\overline{OA}-\overline{OB}  .    \overline{OA}+\overline{OB}=(2;10;-2)\ ,\ \ \overline{OA}-\overline{OB}=(12;-4;-8)  .

Выбираем направляющий вектор  биссектрисы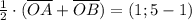  \frac{1}{2}\cdot (\overline{OA}+\overline{OB})=(1;5-1) . Точка, принадлежащая биссектрисе - точка O(0;0;0). Каноническое уравнение биссектрисы:

\dfrac{x-0}{1}=\dfrac{y-0}{5}=\dfrac{z-0}{-1}\ \ \ \Rightarrow \ \ \ \dfrac{x}{1}=\dfrac{y}{5}=\dfrac{z}{-1}              


В треугольнике с вершинами O(0,0,0), A(7,3,–5), B(–5,7,3) проведена биссектриса AОB. Написать ее кан
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
66546654 66546654  20.05.2020 10:32
Царство растений 1 ) выберите три признака , характерные для растений ​...
thero10 thero10  20.05.2020 10:32
Составьте уравнений( неполные, полные)...
femalewolf1309 femalewolf1309  20.05.2020 10:32
На рисунку зображено ромб. Яка градусна міра кута?​...
Людочка13 Людочка13  20.05.2020 10:32
Решите не большая на листочке написать надо​...
sofya15081987 sofya15081987  20.05.2020 10:32
Разложите многочлен на множители: a) 6x^2 - 18x^3. Б) y^2 - 25; в) 2а + a^2-b^2-2^b. r) 5y^2 + 30 y + 45; д) х^3 - 1....
СашаМолорик СашаМолорик  20.05.2020 10:32
Бригада должна была за некоторое время отремонтировать 120 км дороги. Но работа была выполнена на 2 дня раньше срока, так как ежедневно ремонтировали на 3 км больше, чем...
komarovaliza64 komarovaliza64  20.05.2020 10:32
При каком значении ɑ система уравнений имеет бесконечно много решений? 4х + 7у = 6, ɑх – 21у = -18....
kimmatveev kimmatveev  09.04.2020 12:49
Найдите значение выражения 49/a3−49a :(2/7a− 2/7+a ) при a=−35​...
irkaShpagina irkaShpagina  09.04.2020 12:49
Выполни умножение: (2c4−7d2)⋅(2c4+7d2) . Выбери правильный ответ: 2c8−7d4 4c6−49d2 4c8−28c4d2−49d4 4c8−28c4d2+49d4 4c8+28c4d2+49d4 4c8−49d4...
fhehneeggbvfs fhehneeggbvfs  09.04.2020 12:49
Надите при каких значений переменная не имеет смысла алгебраическая дробь 15×m+4/m 2+1​...

Популярные вопросы