В саду растёт черная и красная смородина, всегда 15 кустов. С каждого куста чёрной смородины собрали по 3кг ягод, а с каждого куста красной смородины - по 4кг ягод. Сколько было кустов красной смородины и сколько черной смородины, если всего собрали 51кг ягод?
Другие вопросы по теме Алгебра
Популярные вопросы
- Составить сочинение на тему: Если бы я был Захаром Беркотом, чтобы я пожертвовал...
2 - Выписать 5 предложений с причястиями из учебника по обществознанию за...
3 - надо и как можно быстрее, думаю соответствуют,можно и...
2 - НУЖНО ВСТАВИТЬ СЛОВА В ТЕКСТЫ...
3 - Какие слои украинского населения и почему больше всего поддерживали Реформацию?...
3 - Some или any1. Heve we got_ butter? 2. Have you got_ papier clips ?...
3 - - Варiант 2Від г. Андозька на захід до річки Андога пункт 160,6 м — горизонталь...
2 - Напишите миниатюру (5-8 предложений) Что привлекает читателей в Петре...
2 - Як сделать веску перспиктывнай дз по бел литу...
3 - жизненные ситуации (если можно)изобразить их на графиках спроса. 1-2...
2
Пусть количество черной смородины - х кустов, а красной - у кустов. Тогда из условия следует первое равенство:
х+у=15.
Тогда известно, что из черной собираем по 3 кг, а с красной по 4 кг. И суммарно 51 кг -> 3х+4у=51
Решим систему уравнений:
x+y=15
3x+4y=51
x=15-y
3*(15-y)+4y=51
45+y=51
y=6
тогда х=9
Следовательно, кустов черной смородины было 9 кустов, а красной - 6 кустов.
Отв. 6 кустов, 9 кустов
Кустов красной смородины - 6 штук.
Кустов черной смородины - 9 штук.
Объяснение:
Возьмём количество кустов черной смородины как x; а количество кустов красной смородины как y.
Всего кустов 15 штук, то есть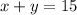 ; также мы знаем, что с кустов собрали ягоды, и их сумма = 51кг, то есть
; также мы знаем, что с кустов собрали ягоды, и их сумма = 51кг, то есть 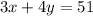 .
.
Получим систему уравнений:
Выразим через
через 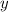 :
:
Подставим это значение вместо во втором уравнении, получим:
во втором уравнении, получим:
Кустов красной смородины - 6 штук.
Следовательно, кустов черной смородины -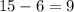 штук.
штук.