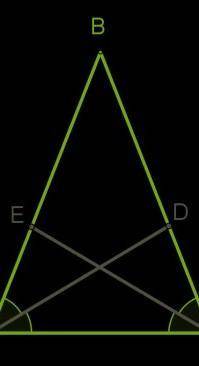
В равнобедренном треугольнике проведены биссектрисы углов, прилежащих к основанию. Определи длину биссектрисы угла ∡A, если длина биссектрисы угла ∡C равна 16 см. Рассмотрим треугольники ΔDAC и Δ
.

(Все углы и стороны нужно записывать большими латинскими буквами.)

1. Углы, прилежащие к основанию равнобедренного треугольника,
. Так как данный треугольник равнобедренный, то ∡B
= ∡BCA.

2. Так как проведены биссектрисы этих углов, справедливо, что ∡
=∡DAC=∡DCE= ∡
.

3. У рассматриваемых треугольников общая сторона
.
Значит, треугольники равны по второму признаку равенства треугольников.
У равных треугольников равны все соответствующие элементы, в том числе стороны
=
.

Длина искомой биссектрисы
см​

marsianin121    2   15.12.2020 14:47    21