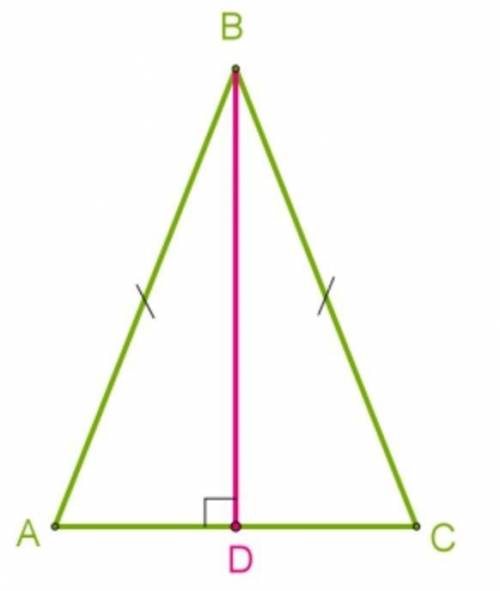
В равнобедренном треугольнике ABC проведена высота к основанию AC, длина основания равна 44 см, ∡ABD=39°. Определи длину отрезка AD и величину углов ∡CBD и ∡ABC.

 

AD =  см;

 

∡CBD = °;

 

∡ABC = °.

​

Для решения данной задачи, нам понадобится знание о свойствах равнобедренного треугольника и о свойствах высоты.

Свойства равнобедренного треугольника:
1. В равнобедренном треугольнике две стороны равны.
2. В равнобедренном треугольнике два угла при основании равны.
3. Высота, проведенная из вершины равнобедренного треугольника, является медианой и биссектрисой угла при основании.
4. Высота, проведенная из вершины равнобедренного треугольника, делит основание на две равные части.

Дано, что треугольник ABC - равнобедренный треугольник, основание AC равно 44 см, угол ABD равен 39°.

1. Найдем длину отрезка AD:
Используя свойства равнобедренного треугольника, мы знаем, что высота, проведенная из вершины, делит основание на две равные части. Значит, отрезок AD равен половине основания AC (половина от 44 см), то есть AD = 44/2 = 22 см.

Ответ: AD = 22 см.

2. Найдем величину угла CBD:
Мы знаем, что высота, проведенная из вершины, является медианой и биссектрисой угла при основании. Значит, угол CBD равен углу ABD (по свойству равнобедренного треугольника), а значит, CBD = ABD = 39°.

Ответ: ∡CBD = 39°.

3. Найдем величину угла ABC:
Мы знаем, что в равнобедренном треугольнике два угла при основании равны. Значит, угол ABC равен углу CBA. Так как сумма углов треугольника равна 180°, угол CBA = (180 - ∡ABC)/2 (по свойству равнобедренного треугольника).

Заменим ∡ABC в формуле:
∡ABC = 180 - (∡ABC + ∡CBA)
2∡ABC = 180 - ∡CBA
∡ABC = (180 - ∡CBA)/2

Заменим ∡CBA по свойству равнобедренного треугольника:
∡CBA = ∡ACB

∡ABC = (180 - ∡ACB)/2

Ответ: ∡ABC = (180 - ∡ACB)/2.

Найдем величину угла ∡ACB:
Сумма углов треугольника ABC равна 180°. Значит, ∡ABC + ∡BAC + ∡ACB = 180°.
∡ABC + ∡ABC + ∡ACB = 180° (по свойству равнобедренного треугольника).
2∡ABC + ∡ACB = 180°.
Заменим ∡ABC по предыдущему ответу:
2((180 - ∡ACB)/2) + ∡ACB = 180°.
180 - ∡ACB + ∡ACB = 180°.
180 = 180°.

Ответ: ∡ACB = 180°.

В результате:
AD = 22 см,
∡CBD = 39°,
∡ABC = (180 - ∡ACB)/2,
∡ACB = 180°.

Пожалуйста, обратитесь за дополнительной информацией, если требуется.