В пространстве функций, даны четыре функции. Является ли они линейно независимыми?
с решением. Нужно подробное описание решения.
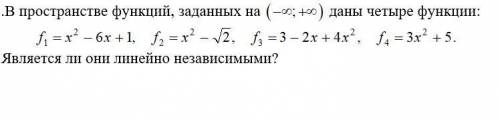
Другие вопросы по теме Алгебра
Популярные вопросы
- «Борьба Северо-Западной Руси против экспансии с Запада» Задание...
2 - Для погружения в воду куска воска массой 7,2гк нему привязали металлическую...
2 - ОТВЕТЫ Какое название носил наиболее плодородный регион Европейской...
3 - Когда учащиеся узнали, что алюминий вытеснять другие металлы из...
2 - Из алкена в диены. Из диен а алкены....
1 - Выберите правильный ответ.В каких координатных четвертях располагается...
1 - D) После неупругого удара двух тел с соотношением масс m1/m2=4,...
3 - Решите уравненияx(y+z) -2y-2z=2b(x-y)+y-x=a(b-c) -4b+4c=ab+ac-b-c=...
1 - Можно ли считать, что выявленные вами при носят относительный характер....
2 - Что стало главной причиной русско-японской войны? 1) Противоречия...
3
ДА
Объяснение:
f1(x) = x^2 - 6x + 1; f2(x) = x^2 - √2; f3(x) = 4x^2 - 2x + 3; f4(x) = 3x^2 + 5
Система функций линейно независима, если ни одну из функций нельзя представить в виде линейной комбинации остальных функций.
То есть вот такого равенства не должно быть:
f1(x) = C2*f2(x) + C3*f3(x) + C4*f4(x)
Мы здесь это и наблюдаем: ни одну функцию нельзя представить в виде комбинации остальных функций.
Проще всего это проверить так: f1(x)/f2(x) ≠ const
Поэтому ДА, они независимы.