В партии из 12 деталей 9 стандартных. Найти вероятность того, что среди 5 наудачу взятых деталей 2 стандартных.

Ответы

KSUMOKLOKOVA 15.10.2020 11:06

$\frac{2}{33}$

Объяснение:

Вероятность по классической формуле равна: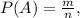 $P(A) = \frac{m}{n},$ где A - событие; P(A) - вероятность этого события; n - общее количество событий , а m - количество событий, которые событию A.

1) Сначала найдём общее количество исходов n - это число выбрать наудачу любые 5 деталей из 12 имеющихся. Несомненно, что если я в правой руке буду держать 3 детали, а в правой - 2, или наоборот, то результат того, когда мы взяли в руки детали и как именно, будет несущественным. Поэтому число всех исходов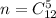 $n = C_{12}^5$ .

2) Перейдем теперь к число событиям событию A (т.е. к m). Чтобы число m благоприятсвовало событию A, нужно чтобы из 5 наудачу взятых деталей 2 были стандартными, а 3 - нестандартных.

Стандартных деталей всего 9, а число выбрать из 9 стандартных деталей только 2 (стандартных) равно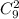 $C_{9}^2$ .

Нестандартных деталей всего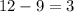 12-9=3 , а число выбрать из 3 нестандартных те же 3 нестандартных равно $C_{3}^3$ .

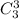3) Если первое действие можно выполнить а второе действие то все действия могут быть выполнены правило умножения). Пусть первое действие это выбирание 2 стандартных деталей из 9 (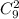 $C_{9}^2$ ), а второе действие - выбирание 3 нестандартных деталей из 3 ( 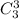$C_{3}^3$ ), тогда всего выбрать 2 стандартные детали из 9 и 3 нестандартные детали из 3 будет: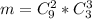 $m = C_{9}^2 * C_{3}^3$

4) Тогда искомая вероятность равна:

$P(A) = \frac{m}{n}= \frac{ C_{9}^2 * C_{3}^3}{C_{12}^5} = \frac{\frac{9!}{2!*7!} }{\frac{12!}{5!*7!} } = \frac{9!}{2!*7!} * \frac{5!*7!}{12!} = \frac{9!}{1*2*7!} * \frac{1*2*3*4*5*7!}{1*2*...*9*10*11*12} = \frac{3*4*5}{10*11*12} = \frac{2}{33} .$