В ответе укажите все целые решения неравенства.
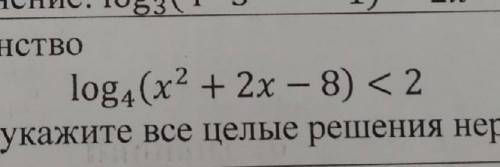
Другие вопросы по теме Алгебра
Популярные вопросы
- Причины не популярности бориса годунова...
3 - Сколько молекул и атомов содержится 1)в 10 моль водорода 2)в...
2 - Арман может выкопать колодец за 6 дней.данияр может выкопать...
1 - Составить формулы солей: фторид алюминия , хлорид ртути , бромид...
1 - Вкаком из перечисленных случаев тело нельзя считать материальной...
1 - Школьники пошли в поход. за 2 часа они километров. найдите x,...
1 - Что объединяет эти личности? василий васильевич тёмный, юрий...
1 - Составить два предложения по языку вопросительные.одно с местоимением...
1 - Корабль, который находится в точке 40° ю.ш. 20° в.д., потерпел...
2 - Сообщение на тему меры предосторожности при общении с инфекционными...
2
Объяснение:
ОДЗ x²+2x-8>0
решим неравенство методом интервалов
x² + 2x - 8 = 0
Найдем дискриминант квадратного уравнения:
D = b² - 4ac = 2²2 - 4·1·(-8) = 4 + 32 = 36
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x₁ = (-2 - √36)/ 2·1 = ( -2 - 6)/ 2 = -8 /2 = -4
x₂ = (-2 + √36 )/2·1 =( -2 + 6)/ 2 = 4/ 2 = 2
(-∞)(-4)2(+∞)
+ - +
x∈(-∞;-4)∪(2;+∞) - это ОДЗ
log₄(x²+2x-8)<2
x²+2x-8<4²
x²+2x-8<16
x²+2x-8-16<0
x²+2x-24<0
решим неравенство методом интервалов
x² + 2x - 24 = 0
Найдем дискриминант квадратного уравнения:
D = b² - 4ac = 2² - 4·1·(-24) = 4 + 96 = 100
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x₁ = ( -2 - √100 )/2·1 = ( -2 - 10)/ 2 = -12 /2 = -6
x₂= ( -2 + √100)/ 2·1 = ( -2 + 10)/ 2 = 8 / 2 = 4
(-∞)(-6)4(+∞)
+ - +
x∈(-6;4)
c учетом ОДЗ x∈(-∞;-4)∪(2;+∞)
x∈(-6;-4)∪(2;4)
выбираем целые значения
х={-5;3}