1. Алгебра
  2. В геометрической прогрессии

В геометрической прогрессии сумма первых пяти членов равна 121, сумма первых десяти равна 29524. Укажи, чему равна сумма членов этой прогрессии с одиннадцатого по семнадцатый включительно. 65740554
64570554
67540575
64540557

математик222 математик222    3   15.12.2020 07:15    0

Ответы
Vika3499 Vika3499  14.01.2021 07:15

Сумма первых n членов геометрической прогрессии:

S_n=\dfrac{b_1(q^n-1)}{q-1}

Распишем сумму первых пяти членов и сумму первых десяти членов:

S_5=\dfrac{b_1(q^5-1)}{q-1} =\dfrac{b_1}{q-1} \cdot (q^5-1)=121

S_{10}=\dfrac{b_1(q^{10}-1)}{q-1} =\dfrac{b_1}{q-1} \cdot (q^{10}-1)=29524

Разделим второе равенство на первое:

\dfrac{\dfrac{b_1}{q-1} \cdot (q^{10}-1)}{\dfrac{b_1}{q-1} \cdot (q^5-1)} =\dfrac{29524}{121}

\dfrac{q^{10}-1}{q^5-1}=244

q^{10}-1=244(q^5-1)

q^{10}-1=244q^5-244

q^{10}-244q^5+243=0

Решим уравнение относительно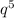 q^5. Так как сумма коэффициентов равна 0, то:

q^5=1\Rightarrow q=1

q^5=243\Rightarrow q=\sqrt[5]{243} =3

Первый случай c q=1 не реализуется, так как в этом случае сумма первых десяти членов была бы в 2 раза больше, чем сумма первых пяти членов.

Значит,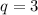 q=3.

Выразим из первого условия выражение для дроби:

\dfrac{b_1}{q-1} =\dfrac{121}{q^5-1}=\dfrac{121}{3^5-1}=\dfrac{121}{242}=\dfrac{1}{2}

Запишем выражение для искомой суммы:

S_{11-17}=S_{17}-S_{10}=\dfrac{b_1(q^{17}-1)}{q-1} -S_{10}=\dfrac{b_1}{q-1} \cdot (q^{17}-1)-S_{10}

Находим сумму:

S_{11-17}=\dfrac{1}{2} \cdot (3^{17}-1)-29524=64540557

ответ: 64540557

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
markinaalisa2003 markinaalisa2003  23.04.2020 15:19
Как выразит y через x в уравнении 0.3x + 0.8y = -6...
кирилл2127 кирилл2127  23.04.2020 15:19
Дитячий майданчик має форму прямокутника, площа якого дорівнює 144м². Одна його сторона на 7м більша, ніж інша. На дитячому майданчику необхідно побудувати бордюр. У магазині...
ayzilyamannano ayzilyamannano  23.04.2020 15:19
Реши систему уравнений алгебраического сложения....
artiushkin213 artiushkin213  23.04.2020 15:19
Побудувати кут косинус якого дорівнює ​...
NoRMTaKK NoRMTaKK  23.04.2020 15:19
Определи, будет ли уравнение с двумя переменными 6x+9y−5=0 линейным?ответ: будет ленейным, не будет ленейнымуравнение с двумя переменными 6x+9y−5=0 будет линейнымне будет...
laparoscopic laparoscopic  23.04.2020 15:19
1. Докажите, что значение выражения 39+38 +37+2+36 делится на 41 безостатка.2.Сколько целых решений имеет неравенство | 8-4x| = 32?3. Если cos a = - п a , то найдите tgа.4....
raniskarimov2 raniskarimov2  23.04.2020 15:19
Реши систему неравенств: {^2−5+4≥0 {^2+17+72 0 Решите это неравенство...
artem0395 artem0395  23.04.2020 15:19
Представь в виде произведения 1x-x^36 q^12​...
nastenamolova0 nastenamolova0  23.04.2020 15:19
решить билеты с объяснением...
seSSS seSSS  09.02.2022 04:41
A-5 B-5 C-7 Решите , + отмечу как лучший ответ....

Популярные вопросы