Відомо, що три натуральні числа є послідовними членами геометричної прогресії. Третє дорівнює 12, і якщо узяти (-36) замість 12, то ці три числа будуть послідовними
членами арифметичної прогресії. Знайдіть суму цифр першого числа.
​

Відповідь:

9

Пояснення:

Нехай перше та друге числа — x та y відповідно. Отже, числа x, y і 12 утворюють геометричну прогресію, а числа x, y і -36 — арифметичну.

Скористаємося основними властивостями цих прогресій. Квадрат кожного члена геометричної дорівнює добутку сусідніх. Зокрема для члена y,

Кожен член арифметичної прогресії дорівнює середньому арифметичному сусідніх. Зокрема для того ж члена y,

.

Звідси .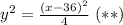

Ліві частини рівнянь (*) і (**) збігаються, тому прирівняємо праві та знайдемо x:

Якщо перше з розглядуваних чисел — 12, то друге дорівнює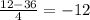 . Воно не натуральне й не задовольняє умові. Якщо ж x=108, то 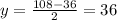, що цілком відповідає умові задачі.

Тоді сума цифр першого числа 1+0+8=9.