1. Алгебра
  2. В арифметической прогрессии

В арифметической прогрессии -4;2;-2;0.2 Найти а11 и

Bogataer1 Bogataer1    3   01.03.2020 10:19    0

Ответы
айдын23 айдын23  11.10.2020 15:50

Объяснение:

Если   -4 ; 2 ; -2 ; 0,2 ; ...  является арифметической прогрессией, то каждый последующий член должен отличаться от предыдущего на одно и то же число.

a_2-a_1=2-(-4)=6\\\\a_3-a_2=-2-2=-4\; \; ,\; \; -4\ne 6\\\\a_4-a_3=0,2-(-2)=2,2\; \; ,\; \; \; \; 2,2\ne -4\; ,\; \; 2,2\ne 6

Как видим, это свойство арифм. прогрессии не выполняется .

Если считать, что задана геометрическая прогрессия, то каждый последующий член должен быть равен  предыдущему члену, умноженному на одно и то же число q .

b_{n}=b_{n-1}\cdot q\; \; \Rightarrow \; \; \; q=\frac{b_{n}}{b_{n-1}}\\\\\frac{a_2}{a_1}=\frac{2}{-4}=-\frac{1}{2}=q\\\\\frac{a_3}{a_2}=\frac{-2}{2}=-1\; \; ,\; \; -1\ne -\frac{1}{2}\\\\\frac{a_4}{a_3}=\frac{0,2}{-2}=-0,1\; \; ,\; \; -0,1\ne -1\; \; ,\; \; -0,1\ne -\frac{1}{2}

Здесь тоже не выполняется свойство геом. прогрессии, так как число q должно быть одним и тем же.

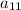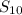Поэтому вычислить ни  a_{11}  , ни  S_{10}  вычислить невозможно .

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
aleksapopov1 aleksapopov1  29.11.2021 05:24
Последовательность задана формулой аn=2n+6 определите номер члена последовательности равного...
хэюяфй хэюяфй  29.11.2021 05:17
Функция задана формулой у = х² - 9. Найдите значение функции, если аргумент равен -2....
VicusiaKoval VicusiaKoval  29.11.2021 05:14
Функция задана формулой у = 2х + 3. Найдите значение аргумента, если значение функции -1...
Amdrek Amdrek  29.11.2021 05:05
Используя график, определите какое значении принимает функция пои значении аргумента 3...
bagaeva02 bagaeva02  29.11.2021 05:03
3.101. Прямая 2х + by = 3 проходит через точку пересечения прямых = 0и - 2x + Зу = -12. Найдите b. 4х – Зу = 0...
Yanis2286 Yanis2286  04.09.2021 19:38
11. Найдите корни уравнения: а) – 5х – 24 = 0; в) 0,5х2 + 2х + 2 = 0; б) х2 – 13х + 42 = 0; г) 0,1х2 – 0,6х + 0,9 = 0. б...
SmokeSivunenko SmokeSivunenko  04.09.2021 19:43
Обчисліть значення числового виразу.Найдите ответ...
рот40 рот40  04.09.2021 19:44
X(y-z)+y(z-x)=z(y-x) доведіть тотожність ‼️‼️‼️...
Zubkub Zubkub  04.09.2021 19:45
мне очень надокому не сложно...
Вадим220404 Вадим220404  04.09.2021 19:46
Постройте график функции заданной формулой у=3х+1...

Популярные вопросы