ІВ
АЛГЕБРА 9 КЛАСС. ГЕОМЕТРИЧНА ПРОГРЕСІЯ
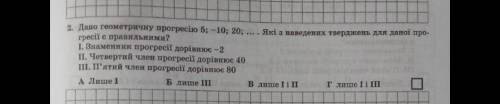
Другие вопросы по теме Алгебра
Популярные вопросы
- 5. Рассмотри картинку ребятам составить предложения. Запиши их. ТруКто? иличто?что...
3 - 3 3.3. Қабырғасы 1) 1,2 см; 2) дм; 34болатын шаршының ауданын табыңдар.2)дм; 3)...
1 - САМОСТІЙНА РОБОТА No 22Порівняння раціональних чиселСтавлю 5 звезд...
3 - СПИШИТЕ ТЕКСТ, вставьте пропущенные буквы. После переписанного текста, выпишите...
1 - Ребята, мы проолжаем тему Царские курганы Шиликты и Бесшатыр посмотрите видео урок,...
3 - Спишите, вставляя пропущенные буквы, раскрывая скобки и расставляя запятые. Наконец(то)...
3 - Задание 1 Раскройте скобки, выберите нужную форму. 1.На смежное предприятие в качестве...
1 - Площадь картофельного поля 575 м². Длина картофельного поля 25 м. Найдите периметр...
3 - Дан треугольник ABC. Если AB + BC = (2 +2√2) см, ∠A = 45° и ∠C = 30°, то найди длину...
2 - 1200 5 Есепте. .64 мФигураның боялған бөлігінің ауда-нын тап. Оны әртүрлі тәсілдерменорындауға...
2
Б) лише 1 наверное так) (наверное)
По условию задачи, дана геометрическая прогрессия bn, первые три члена которой равняются:
b1 = 5;
b2 = -10;
b3 = 20.
Найдем знаменатель q данной геометрической прогрессии. Для этого воспользуемся соотношением b2 = b1*q. Подставляя в данное соотношение значения b1 и b2 из условия задачи, получаем уравнение:
5*q = -10.
Находим q из этого уравнения:
q = -10/5;
q = -2.
Для того, чтобы убедиться, действительно ли данная последовательность является геометрической прогрессией, проверяем выполняется ли соотношение b3 = b2*q. Поскольку 20 = (-10)*(-2), то данная последовательность является геометрической прогрессией.
Находим b4:
b4 = b3*q = 20*(-2) = -40.
Находим b5:
b5 = b5*q = (-40)*(-2) = 80.
Находим теперь сумму первых пяти членов данной прогрессии:
b1 + b2 + b3 + b4 + b5 = 5 - 10 + 20 - 40 + 80 = 55.
ответ: сумма первых пяти членов данной прогрессии равна 55.