, уже полчаса бьюсь над этим, не понимаю почему не получается( Нужно решить данную систему уравнений с метода замены переменных. Если не сложно объясните ход своего решения.

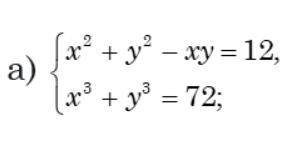
, уже полчаса бьюсь над этим, не понимаю почему не получается( Нужно решить данную систему уравнений

Ответы

F777FF 06.05.2021 15:34

Відповідь:

$\left \{ {{x^2+y^2-xy=12} \atop {x^3+y^3=72}} \right. \\1)x^3+y^3=(x+y)(x^2-xy+y^2)\\\\$

делим 2ое на 1ое

$\frac{(x+y)(x^2-xy+y^2)}{x^2+y^2-xy}= \frac{72}{12} \\\\x+y=6\\x=6-y\\\\(6-y)^2+y^2-y(6-y)=12\\36-12y+y^2+y^2-6y+y^2-12=0\\3y^2-18y+24=0\\D=324-288=36=6^2\\x_{1} =4\\x_{2} =2\\\\x_{1}=4\\y_{1}=2\\\\x_{2}=2\\y_{2}=4$

Пояснення:

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

maxkostin29rus 21.05.2019 09:50

A=v-v0/t нужно выразить t. получается t =v-vo/a т_т...

krav4enkom 21.05.2019 09:50

Для 4 порций приправы требуется 1/3 чайной ложки соли, 1/4 чайной ложки перца и 1/2 чайной ложки гвоздики. сколько соли. перца и гвоздики потребуется для 30 порций...

Эхэхэхэхэхэх 10.08.2019 11:40

Найдите точку пересечение графиков линейной функции у=х-2 и у=3-2х...

шгилтдтдьжжь 10.08.2019 11:40

Какое количество воды надо добавить к 3 л 36 %-го раствора соли,чтобы получить 24%-й раствор?...

1delicious1apple 10.08.2019 11:40

Каким видит абай искандера? в поэме искандер 10...

014UCHENIK014 10.08.2019 11:40

Бегун выполнил тренера за 3 дня тренеровок . за первый день он выполнил 25% всего , а во второй 5/12 остатка , а в третий (день наибольшей нагрузки) пробежал последние 35 кг . сколько...

kappa161 21.04.2021 12:03

510. Для ремонту будинку запросили кількох робітників. Якщо їх буде на 3 чоловіки менше, то термін виконання роботи збіль- шиться на 6 днів; якщо ж робітників буде на 2 чоловіки...

Максим56065 21.04.2021 12:01

УМОЛЯЮ ВАС ЛЮДИИИ МОДЕРАТОРЫ И УЧЁНЫЕ преобразуйте выражение в дробь 1)n^2+2/b2)a/b+x3)n^3+3/bупрастите выражение 1)в/2у-а/2x^22)3x/ab+2y/2a^2b-4/ba^2b^2...

pOMOGITPLZ1 21.04.2021 12:00

решить ! Алгебра 10 класс...

АлексейGrigorjew 21.04.2021 11:58

=((1-i)/(-2-2i))^-4 Выполнить действия в тригонометрической форме и представить результат в тригонометрической, алгебраической и показательной формах...

Популярные вопросы