Установите соответствие между уравнениями (1 - 4) и их решениями (а - е).
(установіть відповідність між рівняннями ( 1 – 4 ) та їх розв'язками ( а – е). )
Другие вопросы по теме Алгебра
Популярные вопросы
- уже 1 час не могу понять ...
2 - Почему светится люминофор стеклянной лампы дневного света, экран телевизора?...
3 - 1. Как поэт рисует родную природу? 2. Какие поэтические средства использует...
3 - За температури 24•С повітря має відносну вологість 70%. Скільки води...
2 - 5 класс. страница 154 1-topshiriq. составить текст на тему Kitob. 5-6...
3 - на скільки зміниться внутрішня енергія 160 г кисню при збільшенні його...
2 - 4 Изложи схожие и отличительные черты борьбы Саттарханаи Бабека:...
2 - Написать мини-сочинение на тему Что общего между обособленными и уточняющими...
2 - определите работу которую совершает газ при изобарическом нагревании...
3 - ВО всех предложения нужно расставить знаки препинания...
3
ответ: 1-Б , 2 - Г , 3 - E , 4 - A .
Объяснение:
ответ: Б)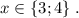
ответ: Г)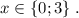
ответ: Е)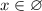 .
.
ответ: А)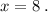
1 - Б
2 - Г
3 - Е
4 - А