Упростите выражение (k+1)k + 2(k+1) до выражения (k+2)(k+1) с очень подробные решением. Я тупо не понимаю, поэтому очень очень подробно.

Как можно заметить, тут есть два слагаемых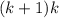 и 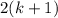с двумя одинаковыми множителям - скобками 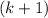. Вынесем их за скобку.

Это делается по аналогии с вынесением переменной за скобки, только вместо переменной тут выносится целая скобка.

Теория:

Распределительный закон умножения относительно сложения: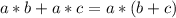

(k+1)*к+2(к+1)

У Вас одинаковая скобка (к+1), я ее выделил жирным шрифтом.

Ее мы вынесем  за скобку. Эдак, скобку за скобку. Чтобы понять, что останется внутри второй скобки, надо каждое слагаемое разделить на ту скобку, которую Вы вынесли, т.е. на (к+1)

Итак, (к+1)*к/(к+1)=к, а от второго слагаемого останется 2*(к+1)/(к+1)=2, все, что попадет во вторые скобки, я подчеркнул.

Итак, (k+1)*к +2(к+1)=(к+1)*(к+2)

Изменим порядок следования, получим именно то, что Вам надо.

(k+1)*к+2(к+1)=(к+2)(к+1)*