упростить и вычислить 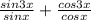
если
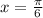

Другие вопросы по теме Алгебра
Популярные вопросы
- Чи може подавати приклад героїзму вигаданий персонаж...
2 - Построить равнобедренный прямоугольный треугольник по двум катетам...
2 - Решить (√12-3,5)(5-4х)(3√5-7)меньше 0...
3 - Как дышат животные в воде и на суше?...
1 - Твой брат учится в кадетсом классе.напиши ему на обратной стороне...
3 - Начертите произвольный четырёхугольный abcd и проведите прямые ac...
1 - Пешеход за 4 ч км.с какой скоростью он шел...
2 - Начерти три треугольника с разными длинами сторон так ,чтобы в одном...
2 - Расставит скобки так,что бы получилось 6*9-3*2-8=64 48: 4+2*4-1=31...
1 - Баба яга кощей бессмертный змей горыныч и соловей разбойник выйграли...
2
При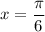 :
:
ответ: 2