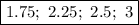Упети есть калькулятор, на котором есть кнопка f. при нажатии на кнопку f, к числу прибавляется его дробная часть (например, из числа 2,36 получается число 2,72). петя нажал на кнопку f два раза и получил число 3. с какого положительного числа он мог начать?

если ответов несколько, введите их все.

Ответы

8Мария11 23.08.2020 12:09

Задачу можно понимать 2 разными по итогу решим оба варианта)

1-ый вариант, когда каждый раз прибавляется дробная часть исходного числа.

2-ой вариант, когда прибавляется дробная часть последнего полученного числа.

Решаем по 1-ому варианту.

Представим число как сумму целой и дробной части $x=[x]+\{x\}$

, так вот, дробной части у нас аж 3, так как Петя два раза её прибавляет

Тогда получается такое равенство: $[x]+3\{x\}=3; \ [x] \in \mathbb{N}$

Нулевой икс в целой части нет смысла рассматривать, так как дробная часть ограничена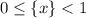 $0\leq\{x\}$

Учитываем, что целая часть числа целая, значит, и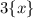 $3\{x\}$ - число тоже целое. Это возможно только в том случае, если 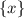$\{x\}$ или просто целое число (1 не может быть, только 0) или дробь со знаменателем 3, то есть рассматриваем

$\displaystyle 1) \{x\}=0 \Rightarrow [x]=3-3\{x\}=3 \Rightarrow x=3 \\ 2) \{x\}=\frac{1}{3} \Rightarrow [x]=3-3\cdot \frac{1}{3}=3-1=2 \Rightarrow x=2\frac{1}{3} \\ 3) \{x\}=\frac{2}{3} \Rightarrow [x]=3-3\cdot \frac{2}{3}=3-2=1 \Rightarrow x=1\frac{2}{3}$

x=3 пойдет в любом случае, а вот остальные два дробных ответа идут только в том случае, если калькулятор поддерживает арифметику с округлениями (такие, естественно, существуют, у меня дома есть такой, инженерный, он чуть поумнее стандартного калькулятора, причем необязательно программируемый).

Соответственно, начать он с этих чисел мог с инженерного калькулятора в том числе и после некоторых дробных вычислений, так что условие задачи выполнено.

Можно, конечно, и проверить эти числа ради интереса

$\displaystyle 3+0+0=3 \\ 2\frac{1}{3}+\frac{1}{3}+\frac{1}{3}=3 \\ 1\frac{2}{3}+\frac{2}{3}+\frac{2}{3}=3$

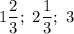
ответ: $\displaystyle 1\frac{2}{3}; \ 2\frac{1}{3}; \ 3$

Решаем по 2-му варианту.

Первое число $x=[x]+\{x\}$

Второе число $[x]+\{x\}+\{x\}=[x]+2\{x\}$

А далее все зависит от дробной части второго числа.

Если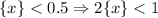 $\{x\}$ , то есть вся дробная часть прибавится и получится третье число

$[x]+2\{x\}+2\{x\}=[x]+4\{x\}$

$[x]+4\{x\}=3; \ 4\{x\} \in \mathbb{Z}; \ 0 \leq \{x\}$

Два числа получили.

Теперь рассматриваем случай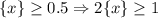 $\{x\}\geq 0.5 \Rightarrow 2\{x\}\geq 1$

То есть потенциальная дробная часть получается больше единицы, значит, необходимо эту единицу оттуда убрать и добавить к целой части, получается вот что:

$[x]+2\{x\}=[x]+1+(2\{x\}-1)$ , где в скобках дробная часть второго числа

Теперь третье число:

$[x]+1+(2\{x\}-1)+2\{x\}-1=[x]+4\{x\}-1=3 \Rightarrow \\ \Rightarrow [x]+4\{x\}=4; \ 0.5 \leq \{x\}$

Получили ещё 2 значения, их можно не проверять, но я все же напишу цепочки для достоверности:

$\displaystyle 1) \ 1.75 \xrightarrow {+0.75} 2.5 \xrightarrow {+0.5} 3; \\ 2) \ 2.25 \xrightarrow {+0.25} 2.5 \xrightarrow {+0.5} 3; \\ 3) \ 2.5 \xrightarrow {+0.5} 3 \xrightarrow {+0.0} 3; \\ 4) \ 3 \xrightarrow {+0.0} 3 \xrightarrow {+0.0} 3$