умоляю умоляю умоляю умоляю
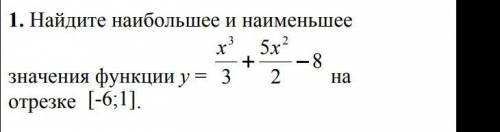
Другие вопросы по теме Алгебра
Популярные вопросы
- очень нужно. 1) i go to school in... 2) i go to school by... 3) i...
2 - зделать соч 6 класспо математике...
2 - О чем рассказывается в произведении алиса в стране загадок...
1 - Бір ауылдан бір бағытта екі велосипедші бір уақытта жолға шықты.Біріншісі-16км/сағ,ал...
2 - Охарактеризуйте барина охотника жестами,мимикой одежной поведением...
3 - с 5,6 и 7 заданием Отмечу как лучший...
1 - Определи порядок действия .реши 345*2+584:4-(1000874)=...
3 - Составь из апорных слов предложения МОЕ ПУТЕШЕСТВИЯ .ПУТИШЕСТВИЯ.страны...
1 - Картинки:ABCDПредложения :1234...
3 - Абай окуыкатыұсынылып отыр.4. Мәтіндегі сұлу табиаттай сенің өлкеде...
2
Наименьшее - 8
Наибольшее 10
Просто нужно представить 0 и - 6
у наиб = у(-5) = 12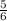
у наим = у(0) = -8
Объяснение:
Функция
Производная функции
y' = x² + 5x
Найдём точки экстремумов
x² + 5x = 0
х(х + 5) = 0
х₁ = 0; х₂ = -5;
В точке х₁ = 0 производная меняет знак с - на +, поэтому х₁ = 0 - точка минимума.
В точке х₂ = -5 производная меняет знак с + на -, поэтому х₂ = -5 - точка максимума.
В интервале х ∈ [-6; 1] находятся и точка максимума х₂ = -5 и точка минимума х₁ = 0 , поэтому наибольшее значение функция будет иметь в точке х₂ = -5, а наименьшее значение а точке х₁ = 0
у наиб = у(-5) = (-5)³/3 + 5 · (-5)²/2 - 8 = -41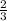 + 62,5 - 8 = 12
+ 62,5 - 8 = 12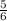
у наим = у(0) = -8